Question

已知拋物線．

（1）求證：無論為任何實數(shù)，拋物線與x軸總有兩個交點；

（2）若為整數(shù)，當關(guān)于x的方程的兩個有理數(shù)根都在與之間（不包括-1、）時，求的值．

（3）在（2）的條件下，將拋物線在x軸下方的部分沿x軸翻折，圖象的其余部分保持不變，得到一個新圖象，再將圖象向上平移個單位，若圖象與過點（0，3）且與x軸平行的直線有4個交點，直接寫出n的取值范圍是                ．

 

Answer 1

【答案】

（1）由無論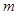為任何實數(shù)，都有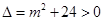即可作出判斷；（2）-1；（3）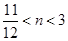

【解析】

試題分析：（1）由無論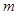為任何實數(shù)，都有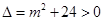即可作出判斷；

（2）由題意可知拋物線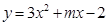的開口向上，與y軸交于（0，-2）點，根據(jù)方程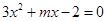的兩根在-1與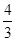之間，可得當x=-1和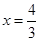時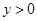，．即可求得m的范圍，再結(jié)合方程的判別式的結(jié)果即可作出判斷；

（3）根據(jù)拋物線的平移規(guī)律即函數(shù)圖象上的點的坐標的特征求解即可.

（1）∵△=，

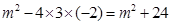∴無論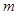為任何實數(shù)，都有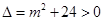

∴拋物線與x軸總有兩個交點；

（2）由題意可知：拋物線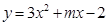的開口向上，與y軸交于（0，-2）點，

∵方程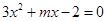的兩根在-1與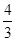之間，

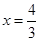∴當x=-1和時，．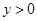

即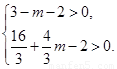 

解得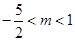

因為m為整數(shù)，所以 m=-2，-1，0

當m=-2時，方程的判別式△=28，根為無理數(shù)，不合題意

當m=-1時，方程的判別式△=25，根為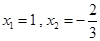，符合題意

當m=0時，方程的判別式△=24，根為無理數(shù)，不合題意

綜上所述m=-1；

（3）n的取值范圍是．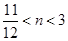

考點：二次函數(shù)的綜合題

點評：此類問題是初中數(shù)學(xué)的重點和難點，在中考中極為常見，一般以壓軸題形式出現(xiàn)，難度較大.