
【題目】在矩形![]() 中,
中,![]() 是
是![]() 的中點,以點
的中點,以點![]() 為直角頂點的直角三角形
為直角頂點的直角三角形![]() 的兩邊
的兩邊![]() 、
、![]() 始終與矩形
始終與矩形![]() 、
、![]() 兩邊相交,
兩邊相交,![]() ,
,![]() ,
,
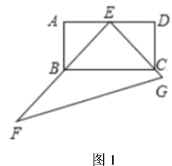
(1)如圖1,當![]() 、
、![]() 分別過點
分別過點![]() 、
、![]() 時,求
時,求![]() 的大小;
的大小;
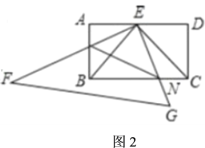
(2)在(1)的條件下,如圖2,將![]() 繞點按順時針方向旋轉,當旋轉到
繞點按順時針方向旋轉,當旋轉到![]() 與
與![]() 重合時停止轉動.若
重合時停止轉動.若![]() 、
、![]() 分別與
分別與![]() 、
、![]() 相交于點
相交于點![]() 、
、![]() .
.
①在![]() 旋轉過程中,四邊形
旋轉過程中,四邊形![]() 的面積是否發生變化?若不變,求四邊形
的面積是否發生變化?若不變,求四邊形![]() 的面積;若要變,請說明理由.
的面積;若要變,請說明理由.
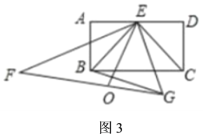
②如圖3,設點![]() 為
為![]() 的中點,連結
的中點,連結![]() 、
、![]() ,若
,若![]() ,當
,當![]() 的長度最小時,求
的長度最小時,求![]() 的值.
的值.
【答案】(1)45°;(2)①不變,4;②![]() .
.
【解析】
(1)證明△AEB≌△DEC(SAS),可得EB=EC,根據等腰直角三角形的性質即可解決問題.
(2)①四邊形BMEN的面積不變.證明△MEB≌△NEC(ASA),推出S△MEB=S△ENC,可得S四邊形EMBN=S△EBC.
②如圖當E,B,O共線時,OB的值最小,作GH⊥OE于H.想辦法求出BH,GH即可解決問題.
解:(1)如圖1中,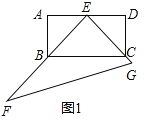
∵四邊形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵AE=DE,
∴△AEB≌△DEC(SAS),
∴EB=EC,
∵∠BEC=90°,
∴∠EBC=45°.
(2)①結論:四邊形BMEN的面積不變.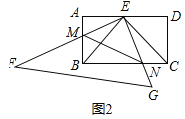
理由:由(1)可知:∠EBM=∠ECN=45°,
∵∠MEN=∠BEC=90°,
∴∠BEM=∠CEN,
∵EB=EC,
∴△MEB≌△NEC(ASA),
∴S△MEB=S△ENC,
∴S四邊形EMBN=S△EBC=![]() ×4×2=4.
×4×2=4.
②如圖當E,B,O共線時,OB的值最小,作GH⊥OE于H.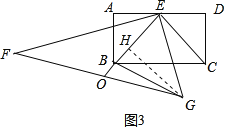
∵OF=OG,∠FEG=90°,
∴OE=OF=OG=4,
∵∠F=30°,
∴∠EGF=60°,
∴△EOG是等邊三角形,∵GH⊥OE,
∴GH=2![]() ,OH=EH=2,
,OH=EH=2,
∵BE=2![]() ,
,
∴OB=4-2![]() ,
,
∴BH=2-(4-2![]() )=2
)=2![]() -2,
-2,
∴tan∠EBG=![]() .
.


科目:初中數學 來源: 題型:
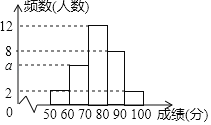
【題目】為了解某次“小學生書法比賽”的成績情況,隨機抽取了30名學生的成績進行統計,并將統計情況繪成如圖所示的頻數分布直方圖,己知成績x(單位:分)均滿足“50≤x<100”.根據圖中信息回答下列問題:
(1)圖中a的值為 ;
(2)若要繪制該樣本的扇形統計圖,則成績x在“70≤x<80”所對應扇形的圓心角度數為 度;
(3)此次比賽共有300名學生參加,若將“x≥80”的成績記為“優秀”,則獲得“優秀“的學生大約有 人:
(4)在這些抽查的樣本中,小明的成績為92分,若從成績在“50≤x<60”和“90≤x<100”的學生中任選2人,請用列表或畫樹狀圖的方法,求小明被選中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
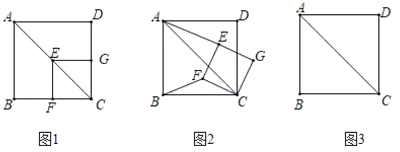
【題目】如圖1,邊長為4的正方形與邊長為![]() 的正方形
的正方形![]() 的頂點
的頂點![]() 重合,點
重合,點![]() 在對角線
在對角線![]() 上.
上.
問題發現
(1)如圖1,![]() 與
與![]() 的數量關系為______.
的數量關系為______.
類比探究
(2)如圖2,將正方形![]() 繞點
繞點![]() 旋轉
旋轉![]() 度(
度(![]() ).請問(1)中的結論還成立嗎?若不成立,請說明理由.
).請問(1)中的結論還成立嗎?若不成立,請說明理由.
拓展延伸
(3)若![]() 為
為![]() 的中點,在正方形
的中點,在正方形![]() 的旋轉過程中,當點
的旋轉過程中,當點![]() ,
,![]() ,
,![]() 在一條直線上時,線段
在一條直線上時,線段![]() 的長度為______.
的長度為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】海鮮門市的某種海鮮食材,成本為10元/千克,每天的進貨量p(千克)與銷售價格x(元/千克)滿足函數關系式![]() ,從市場反饋的信息發現,該海鮮食材每天的市場需求量q(千克)與銷售價格x(元/千克)滿足一次函數關系,部分數據如下表:
,從市場反饋的信息發現,該海鮮食材每天的市場需求量q(千克)與銷售價格x(元/千克)滿足一次函數關系,部分數據如下表:
銷售價格x(元/千克) | 10 | 12 | … | 30 |
市場需求量q(千克) | 30 | 28 | … | 10 |
(已知按物價部門規定銷售價格x不低于10元/千克且不高于30元/千克)
(1)請寫出q與x的函數關系式:___________________________;
(2)當每天的進貨量小于或等于市場需求量時,這種海鮮食材能全部售出,而當每天的進貨量大于市場需求量時,只能售出符合市場需求量的海鮮食材,剩余的海鮮食材由于保質期短而只能廢棄.
①求出每天獲得的利潤y(元)與銷售價格x的函數關系式;
②為了避免浪費,每天要確保這種海鮮食材能全部售出,求銷售價格為多少元時,每天獲得的利潤(元)最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2010年5月1日,第41屆世博會在上海舉辦,世博知識在校園迅速傳播.小明同學就本班學生對世博知識的了解程度進行了一次調查統計,下圖是他采集數據后繪制的兩幅不完整的統計圖(A:不了解,B:一般了解,C:了解較多,D:熟悉).請你根據圖中提供的信息解答以下問題:

(1)求該班共有多少名學生;
(2)在條形統計圖中,將表示“一般了解”的部分補充完整;
(3)在扇形統計圖中,計算出“了解較多”部分所對應的圓心角的度數;
(4)從該班中任選一人,其對世博知識的了解程度為“熟悉”的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分10分)
如圖,臺風中心位于點P,并沿東北方向PQ移動,已知臺風移動的速度為30千米/時,受影響區域的半徑為200千米,B市位于點P的北偏東75°方向上,距離點P 320千米處.

(1) 說明本次臺風會影響B市;
(2)求這次臺風影響B市的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
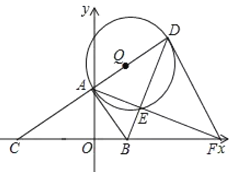
【題目】如圖,在平面直角坐標系![]() 中,已知點
中,已知點![]() ,點B是
,點B是![]() 軸正半軸上一點,連接
軸正半軸上一點,連接![]() ,過點A作
,過點A作![]() ,交
,交![]() 軸于點C,點D是點C關于點A的對稱點,連接
軸于點C,點D是點C關于點A的對稱點,連接![]() ,以
,以![]() 為直徑作
為直徑作![]() 交
交![]() 于點E,連接AE并延長交
于點E,連接AE并延長交![]() 軸于點F,連接DF.
軸于點F,連接DF.
(1)求線段AE的長;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 與
與![]() 相似,求
相似,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=8,BC=4,將矩形沿AC折疊,點D落在點D′處,則重疊部分△AFC的面積為( )

A.6B.8C.10D.12
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com