
【題目】如圖,點A,B,C,D在一條直線上,△ABF≌△DCE.你能得出哪些結論?(請寫出三個以上的結論)
【答案】解:∵△ABF≌△DCE
∴∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;
∴AF∥ED,AC=BD,BF∥CE
【解析】根據全等三角形對應角相等,對應邊相等得出∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;再根據平行線的判定定理及等式的性質得出AF∥ED,AC=BD,BF∥CE。
【考點精析】掌握平行線的判定和全等三角形的性質是解答本題的根本,需要知道同位角相等,兩直線平行;內錯角相等,兩直線平行;同旁內角互補,兩直線平行;全等三角形的對應邊相等; 全等三角形的對應角相等.


科目:初中數學 來源: 題型:
【題目】某商店取廠家選購甲、乙兩種商品,乙商品每件進價比甲商品每件進價多20元,若購進甲商品5件和乙商品4件共需要800元;
(1)求甲、乙兩種商品每件的進價分別是多少元?
(2)若甲種商品的售價為每件100元,乙種商品的售價為每件125元,該商店準備購進甲、乙兩種商品共40件,且這兩種商品全部售出后總利潤不少于900元,則甲種商品最多可購進多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按照有關規定,距高鐵軌道![]() 米以內的區域內不宜臨路新建學校、醫院、敬老院和集中住宅區等噪聲敏感建筑物.如圖是一個小區平面示意圖,長方形
米以內的區域內不宜臨路新建學校、醫院、敬老院和集中住宅區等噪聲敏感建筑物.如圖是一個小區平面示意圖,長方形![]() 為一新建小區,直線
為一新建小區,直線![]() 為高鐵軌道,
為高鐵軌道,![]() 是直線
是直線![]() 上的兩點,點
上的兩點,點![]() 在一條直線上,且
在一條直線上,且![]() .小王看中了
.小王看中了![]() 號樓
號樓![]() 單元的一套住宅,與售樓人員的對話如下:
單元的一套住宅,與售樓人員的對話如下:
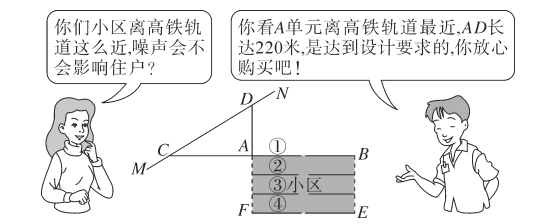
![]() 小王心中一算,發現售樓人員的話不可信,請你用所學的數學知識說明理由;
小王心中一算,發現售樓人員的話不可信,請你用所學的數學知識說明理由;
![]() 若一列長度為
若一列長度為![]() 米的高鐵以
米的高鐵以![]() 千米/時的速度通過,則
千米/時的速度通過,則![]() 單元用戶受到影響的時間有多長?
單元用戶受到影響的時間有多長?
(參考數據:![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖中是拋物線拱橋,P處有一照明燈,水面OA寬4m,從O,A兩處觀測P處,仰角分別為α、β,且tanα= ![]() ,tan
,tan ![]() ,以O為原點,OA所在直線為x軸建立直角坐標系.
,以O為原點,OA所在直線為x軸建立直角坐標系.
(1)求點P的坐標;
(2)水面上升1m,水面寬多少( ![]() 取1.41,結果精確到0.1m)?
取1.41,結果精確到0.1m)?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD和CEFG的邊長分別為m、n,那么△AEG的面積的值( )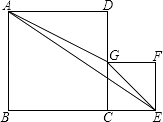
A.與m、n的大小都有關
B.與m、n的大小都無關
C.只與m的大小有關
D.只與n的大小有關
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合題
如圖1,在△ABC中,AB=AC,射線BP從BA所在位置開始繞點B順時針旋轉,旋轉角為α(0°<α<180°)
(1)當∠BAC=60°時,將BP旋轉到圖2位置,點D在射線BP上.若∠CDP=120°,則∠ACD∠ABD(填“>”、“=”、“<”),線段BD、CD與AD之間的數量關系是;
(2)當∠BAC=120°時,將BP旋轉到圖3位置,點D在射線BP上,若∠CDP=60°,求證:BD﹣CD= ![]() AD;
AD;
(3)將圖3中的BP繼續旋轉,當30°<α<180°時,點D是直線BP上一點(點P不在線段BD上),若∠CDP=120°,請直接寫出線段BD、CD與AD之間的數量關系(不必證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從1、2、3、4中任取一個數作為十位上的數字,再從余下的數字中任取一個數作為個位上的數字,那么組成的兩位數是6的倍數的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形紙片ABCD折疊,使點D與點B重合,點C落在C′處,折痕為EF,若AB=1,BC=2,則△ABE和△BC′F的周長之和為( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點![]() 的坐標為
的坐標為![]() ,
,![]() 與
與![]() 軸交于點
軸交于點![]() ,且
,且![]() 為
為![]() 的中點,雙曲線
的中點,雙曲線![]() 經過
經過![]() 、
、![]() 兩點.
兩點.

(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)如圖1,點![]() 在
在![]() 軸上,若四邊形
軸上,若四邊形![]() 是平行四邊形,求點
是平行四邊形,求點![]() 的坐標;
的坐標;
(3)如圖2,在(2)的條件下,動點![]() 在雙曲線
在雙曲線![]() 上,點
上,點![]() 在
在![]() 軸上,若以
軸上,若以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為平行四邊形,試求滿足要求的所有點
為頂點的四邊形為平行四邊形,試求滿足要求的所有點![]() 、
、![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com