
類比、轉化、從特殊到一般等思想方法,在數學學習和研究中經常用到,如下是一個案例,請補充完整.
原題:如圖1,在 中,點E是BC邊上的中點,點F是線段AE上一點,BF的延長線交射線CD于點G,若
中,點E是BC邊上的中點,點F是線段AE上一點,BF的延長線交射線CD于點G,若 ,求
,求 的值。
的值。
(1)嘗試探究
在圖1中,過點E作 交BG于點H,則AB和EH的數量關系是 ,CG和EH的數量關系是 ,
交BG于點H,則AB和EH的數量關系是 ,CG和EH的數量關系是 , 的值是
的值是
(2)類比延伸
如圖2,在原題的條件下,若 則
則 的值是 (用含
的值是 (用含 的代數式表示),試寫出解答過程。
的代數式表示),試寫出解答過程。
(3)拓展遷移
如圖3,梯形ABCD中,DC∥AB,點E是BC延長線上一點,AE和BD相交于點F,若 ,則
,則 的值是 (用含
的值是 (用含 的代數式表示).
的代數式表示).
 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:
| AF |
| EF |
| CD |
| CG |

| CD |
| CG |
| 3 |
| 2 |
| 3 |
| 2 |
| AF |
| EF |
| CD |
| CG |
| m |
| 2 |
| m |
| 2 |
| AB |
| CD |
| BC |
| BE |
| AF |
| EF |
查看答案和解析>>
科目:初中數學 來源: 題型:
| AF |
| EF |
| CD |
| CG |

| AB |
| EH |
| CG |
| EH |
| CD |
| CG |
| 3 |
| 2 |
| 3 |
| 2 |
| AF |
| EF |
| CD |
| CG |
| m |
| 2 |
| m |
| 2 |
| AB |
| CD |
| BC |
| BE |
| AF |
| EF |
查看答案和解析>>
科目:初中數學 來源:2013屆江蘇省阜寧縣九年級第一次調研數學試卷(帶解析) 題型:解答題
在數學學習和研究中經常需要總結運用數學思想方法。如類比、轉化、從特殊到一般等思想方法,如下是一個案例,請補充完整。
題目:如圖1,在平行四邊形ABCD中,點E是BC的中點,點F在線段AE上,BF的延長線交射線CD于點G,若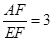 ,求
,求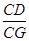 的值。
的值。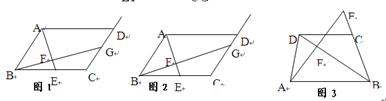
(1)嘗試探究
在圖1中,過點E作EH∥AB交BG于點H,則易求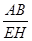 的值是 ,
的值是 ,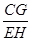 的值是
的值是
,從而確定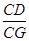 的值是 。
的值是 。
(2)類比延伸
如圖2,在原題的條件下,若 ,則
,則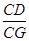 的值是 。(用含m的代數式表示),寫出解答過程。
的值是 。(用含m的代數式表示),寫出解答過程。
(3)拓展遷移
如圖3,在梯形ABCD中,DC∥AB,點E是BC延長線上的一點,AE和BD相交于F,若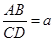 ,
,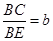 (a>0,b>0),則
(a>0,b>0),則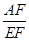 的值是 。(用含a、b的代數式表示)寫出解答過程。
的值是 。(用含a、b的代數式表示)寫出解答過程。
查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇省阜寧縣九年級第一次調研數學試卷(解析版) 題型:解答題
在數學學習和研究中經常需要總結運用數學思想方法。如類比、轉化、從特殊到一般等思想方法,如下是一個案例,請補充完整。
題目:如圖1,在平行四邊形ABCD中,點E是BC的中點,點F在線段AE上,BF的延長線交射線CD于點G,若 ,求
,求 的值。
的值。

(1)嘗試探究
在圖1中,過點E作EH∥AB交BG于點H,則易求 的值是 ,
的值是 , 的值是
的值是
,從而確定 的值是 。
的值是 。
(2)類比延伸
如圖2,在原題的條件下,若 ,則
,則 的值是 。(用含m的代數式表示),寫出解答過程。
的值是 。(用含m的代數式表示),寫出解答過程。
(3)拓展遷移
如圖3,在梯形ABCD中,DC∥AB,點E是BC延長線上的一點,AE和BD相交于F,若 ,
, (a>0,b>0),則
(a>0,b>0),則 的值是 。(用含a、b的代數式表示)寫出解答過程。
的值是 。(用含a、b的代數式表示)寫出解答過程。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com