
【題目】(1)從A地到B地,某甲走直徑AB上方的半圓途徑;乙先走直徑AC上方半圓的途徑,再走直徑CB下方半圓的途徑,如圖1,已知AB=40米,AC=30米,計算個人所走的路程,并比較兩人所走路程的遠近;
(2)如果甲.乙走的路程圖改成圖2,兩人走的路程遠近相同嗎?

【答案】(1)相等;(2)相等.
【解析】試題分析:
(1)甲所走的路徑長為以AB為直徑的半圓長,乙所走的路徑長為以AC和BC為直徑的兩個半圓長的和,然后根據圓的周長公式進行計算,再比較大小即可;
(2)甲所走的路徑長為以AB為直徑的半圓長,乙所走的路徑長為以AC、CD和DB為直徑的三個半圓長的和,然后根據圓的周長公式分別計算他們所走的路徑,再比較大小即可.
試題解析:
(1)BC=AB-AC=10,
甲所走的路徑長=![]() 2π
2π![]() =
=![]() 2π
2π![]() =20π(m),
=20π(m),
乙所走的路徑長=![]() 2π
2π![]() +
+![]() 2π
2π![]() =
=![]() 2π
2π![]() +
+![]() π
π![]() =20π(m),
=20π(m),
所以兩人所走路程的相等;
(2)兩人走的路程遠近相同.理由如下:甲所走的路徑長=![]() 2π
2π![]() =
=![]() πAB,
πAB,
乙所走的路徑長=![]() 2π
2π![]() +
+![]() 2π
2π![]() +
+![]() π
π![]() =
=![]() π(AC+CD+DB)=
π(AC+CD+DB)=![]() πAB,
πAB,
即兩人走的路程遠近相同.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:初中數學 來源: 題型:
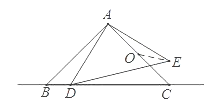
【題目】如圖,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O為AC中點,若點D在直線BC上運動,連接OE,則在點D運動過程中,線段OE的最小值是為( )
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有下列四個命題:
①、同位角相等;②、如果兩個角的和是 180 度,那么這兩個角是鄰補角;
③、在同一平面內,平行于同一條直線的兩條直線互相平行;
④、在同一平面內,垂直于同一條直線的兩條直線互相垂直. 其中是真命題的個數有( )個
A.0B.1C.2D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點P、Q分別是等邊△ABC邊AB、BC上的動點(端點除外),點P從頂點A、點Q從頂點B同時出發,且它們的運動速度相同,連接AQ、CP交于點M.
(1)求證:△ABQ≌△CAP;
(2)當點P、Q分別在AB、BC邊上運動時,∠QMC變化嗎?若變化,請說明理由;若不變,求出它的度數.
(3)如圖2,若點P、Q在運動到終點后繼續在射線AB、BC上運動,直線AQ、CP交點為M,則∠QMC變化嗎?若變化,請說明理由;若不變,直接寫出它的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC的面積是60,請完成下列問題:
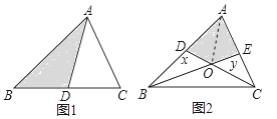
(1)如圖1,若AD是△ABC的BC邊上的中線,則△ABD的面積________△ACD的面積(填“>”“<”或“=”)
(2)如圖2,若CD、BE分別是△ABC的AB、AC邊上的中線,求四邊形ADOE的面積可以用如下方法:連接AO,由AD=DB得:S△ADO=S△BDO , 同理:S△CEO=S△AEO , 設S△ADO=x,S△CEO=y,則S△BDO=x,S△AEO=y由題意得:S△ABE=![]() S△ABC=30,S△ADC=
S△ABC=30,S△ADC=![]() S△ABC=30,可列方程組為:
S△ABC=30,可列方程組為: ![]() , 解得
, 解得![]() ,通過解這個方程組可得四邊形ADOE的面積為________ .
,通過解這個方程組可得四邊形ADOE的面積為________ .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于實數a,我們規定:用符號![]() 表示不大于
表示不大于![]() 的最大整數,稱
的最大整數,稱![]() 為a的根整數,例如:
為a的根整數,例如: ![]() ,
, ![]() .
.
(1)仿照以上方法計算: ![]() = ;
= ; ![]() = .
= .
(2)若![]() =1,寫出滿足題意的x的整數值 .
=1,寫出滿足題意的x的整數值 .
如果我們對a連續求根整數,直到結果為1為止.例如:對10連續求根整數2次 ![]() ,這時候結果為1.
,這時候結果為1.
(3)對100連續求根整數, 次之后結果為1.
(4)只需進行3次連續求根整數運算后結果為1的所有正整數中,最大的是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們學習了勾股定理后,都知道“勾三、股四、弦五”.
觀察:3、4、5;5、12、13;7、24、25;9、40、41;…,發現這些勾股數的勾都是奇數,且從3起就沒有間斷過.
(1)請你根據上述的規律寫出下一組勾股數:________.
(2)若第一個數用字母n(n為奇數,且n≥3)表示,那么后兩個數用含n的代數式分別表示為________和________,請用所學知識說明它們是一組勾股數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com