
【題目】探究與發現:
探究一:我們知道,三角形的一個外角等于與它不相鄰的兩個內角的和.那么,三角形的一個內角與它不相鄰的兩個外角的和之間存在何種數量關系呢?
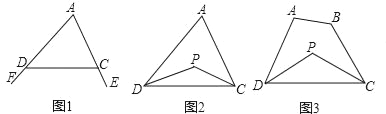
已知:如圖1,∠FDC與∠ECD分別為△ADC的兩個外角,試探究∠A與∠FDC+∠ECD的數量關系.
探究二:三角形的一個內角與另兩個內角的平分線所夾的鈍角之間有何種關系?
已知:如圖2,在△ADC中,DP、CP分別平分∠ADC和∠ACD,試探究∠P與∠A的數量關系.
探究三:若將△ADC改為任意四邊形ABCD呢?
已知:如圖3,在四邊形ABCD中,DP、CP分別平分∠ADC和∠BCD,試利用上述結論探究∠P與∠A+∠B的數量關系.
【答案】探究一:∠FDC+∠ECD=180°+∠A;探究二:∠P=90°+![]() ∠A;探究三:∠P=
∠A;探究三:∠P=![]() (∠A+∠B).
(∠A+∠B).
【解析】
探究一:根據三角形的一個外角等于與它不相鄰的兩個內角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根據三角形內角和定理整理即可得解;
探究二:根據角平分線的定義可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根據三角形內角和定理列式整理即可得解;
∠ACD,然后根據三角形內角和定理列式整理即可得解;
探究三:根據四邊形的內角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可.
解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分別平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD
∠ACD
=180°﹣![]() (∠ADC+∠ACD)
(∠ADC+∠ACD)
=180°﹣(180°﹣∠A)
=90°+![]() ∠A;
∠A;
探究三:∵DP、CP分別平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠BCD
∠BCD
=180°﹣![]() (∠ADC+∠BCD)
(∠ADC+∠BCD)
=180°﹣![]() (360°﹣∠A﹣∠B)
(360°﹣∠A﹣∠B)
=![]() (∠A+∠B).
(∠A+∠B).
故答案為:探究一:∠FDC+∠ECD=180°+∠A;探究二:∠P=90°+![]() ∠A;探究三:∠P=
∠A;探究三:∠P=![]() (∠A+∠B).
(∠A+∠B).


 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案 黃岡創優卷系列答案
黃岡創優卷系列答案科目:初中數學 來源: 題型:
【題目】某縣為落實“精準扶貧惠民政策”,計劃將某村的居民自來水管道進行改造.該工程若由甲隊單獨施工恰好在規定時間內完成;若乙隊單獨施工,則完成工程所需天數是規定天數的1.5倍.如果由甲、乙隊先合作施工15天,那么余下的工程由甲隊單獨完成還需5天.
(1)這項工程的規定時間是多少天?
(2)為了縮短工期以減少對居民用水的影響,工程指揮部最終決定該工程由甲、乙兩隊合作完成.則甲、乙兩隊合作完成該工程需要多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班將舉行“數學知識競賽”活動,班長安排小明購買獎品,下面兩圖是小明買回獎品時與班長的對話情境:

請根據上面的信息,解決問題:
(1)試計算兩種筆記本各買了多少本?
(2)請你解釋:小明為什么不可能找回68元?
查看答案和解析>>
科目:初中數學 來源: 題型:
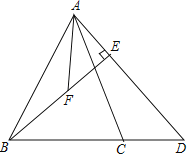
【題目】如圖,在△ABC中,AB=AC,D為線段BC的延長線上一點,且DB=DA,BE⊥AD于點E,取BE的中點F,連接AF.
(1)若AC=![]() ,AE=
,AE=![]() ,求BE的長;
,求BE的長;
(2)在(1)的條件下,如果∠D=45°,求△ABD的面積.
(3)若∠BAC=∠DAF,求證:2AF=AD;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠MON=30°,B為OM上一點,BA⊥ON于A,四邊形ABCD為正方形,P為射線BM上一動點,連結CP,將CP繞點C順時針方向旋轉90°得CE,連結BE,若AB=4,則BE的最小值為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年汶川車厘子喜獲豐收,車厘子一上市,水果店的王老板用2500元購進一批車厘子,很快售完;老板又用4400元購進第二批車厘子,所購數量是第一批的2倍,由于進貨量增加,進價比第一批每干克少了3元.”
(l)第一批車厘子每千克進價多少元?.
(2)該老板在銷售第二批車厘子時,售價在第二批進價的基礎上增加了![]() ,售出
,售出![]() 后,為了盡快售完,決定將剩余車厘子在第二批進價的基礎上每千克降價
后,為了盡快售完,決定將剩余車厘子在第二批進價的基礎上每千克降價![]() 元進行促銷,結果第二批車厘子的銷售利潤為1520元,求
元進行促銷,結果第二批車厘子的銷售利潤為1520元,求![]() 的值。(利潤=售價一進價)
的值。(利潤=售價一進價)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四張小卡片上分別寫有數字1、2、3、4。它們除數字外沒有任何區別,現將它們放在盒子里攪勻.
(1)隨機地從盒子里抽取一張,求抽到數字2的概率.
(2)隨機地從盒子里抽取一張,記下數字后放回再抽取第二張。請你用畫樹狀圖或列表的方法表示所有等可能的結果,并求抽到的數字之和為5的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,已知![]() 是⊙
是⊙![]() 的直徑,
的直徑, ![]() 是
是![]() 上的一個動點(點
上的一個動點(點![]() 與點
與點![]() 、
、![]() 不重合),連接
不重合),連接![]() .
. ![]() 是
是![]() 的中點,作弦
的中點,作弦![]() ,垂足為
,垂足為![]() .
.
(![]() )若點
)若點![]() 和點
和點![]() 不重合,連接
不重合,連接![]() 、
、![]() 和
和![]() .當
.當![]() 是等腰三角形時,求
是等腰三角形時,求![]() 的度數.
的度數.
(![]() )若點
)若點![]() 和點
和點![]() 重合,如圖②.探索
重合,如圖②.探索![]() 與
與![]() 的數量關系并說明理由.
的數量關系并說明理由.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com