Question

【題目】如圖，在△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE，點E在BC上．過點D作DF∥BC，連接DB．

求證：（1）△ABD≌△ACE；

（2）DF=CE．

Answer 1

【答案】（1）證明見解析；（2）證明見解析.

【解析】

（1）求出∠BAD=∠BAC，根據SAS證出△BAD≌△CAE即可；

（2）根據全等推出∠DBA=∠C，根據等腰三角形性質得出∠C=∠ABC，根據平行線性質得出∠ABC=∠DFB，推出∠DFB=∠DBF，根據等腰三角形的判定推出即可．

（1）∵∠BAC=∠DAE，∴∠BAC﹣∠BAE=∠DAE﹣∠BAE，∴∠BAD=∠EAC．在△BAD和△CAE中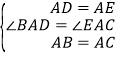，∵，∴△BAD≌△CAE（SAS）；

（2）∵△BAD≌△CAE，∴∠DBA=∠C．

∵AB=AC，∴∠C=∠ABC．

∵DF∥BC，∴∠DFB=∠ABC=∠C=∠DBA，即∠DFB=∠DBF，∴DF=CE．