
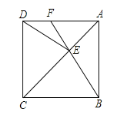
【題目】如圖,正方形ABCD中,點E在對角線AC上,連接EB、ED.
(1)求證:△BCE≌△DCE;
(2)延長BE交AD于點F,若∠DEB=140,求∠AFE的度數.
【答案】(1)、證明過程見解析;(2)、65°.
【解析】
試題分析:(1)、根據正方形的性質可得BC=DC,∠BCE=∠CDE=45°,根據CE=CE得出三角形全等;(2)、根據全等得出∠BEC=∠DEC=70°,根據△BCE的內角和得出∠CBE=65°,根據平行線的性質得出∠AFE=∠CBE.
試題解析:(1)、∵正方形ABCD中,E為對角線AC上一點,
∴BC=DC,∠BCE=∠DCE=45 又∵CE=CE ∴△BCE≌△DCE(SAS)
(2)、由全等可知,∠BEC=∠DEC=![]() ∠DEB=
∠DEB=![]() ×140=70
×140=70
在△BCE中,∠CBE=180―70―45=65
∴在正方形ABCD中,AD∥BC,有∠AFE=∠CBE=65


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】若△ABC與△DEF的相似比是3:2,△DEF的最長邊是6cm,那么△ABC的最長邊是( )
A.4cm
B.9cm
C.4cm或9cm
D.以上答案都不對
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com