
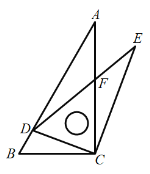
【題目】如圖,兩個大小不同的三角板放在同一平面內(nèi),直角頂點重合于點![]() ,點
,點![]() 在
在![]() 上,
上,![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,若
,若![]() ,
,![]() ,則
,則![]() _________.
_________.
【答案】![]()
【解析】
過點C作CM⊥DE于點M,先證![]() BCD∽
BCD∽![]() ACE,求出AE的長及∠CAE=60°,推出∠DAE=90°,在Rt
ACE,求出AE的長及∠CAE=60°,推出∠DAE=90°,在Rt![]() DAE中利用勾股定理求出DE的長,進一步求出CE的長,再證
DAE中利用勾股定理求出DE的長,進一步求出CE的長,再證![]() AFD∽
AFD∽![]() EFC,利用相似三角形對應(yīng)邊的比相等即可求出
EFC,利用相似三角形對應(yīng)邊的比相等即可求出![]() 的比值.
的比值.
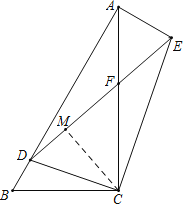
解:如圖,過點C作CM⊥DE于點M,
∵BD=2,AD=8,
∴AB=BD+AD=10,
∵在Rt△ABC中,∠BAC=30°,∠B=90°﹣∠BAC=60°,
∴BC=![]() AB=5,AC=
AB=5,AC=![]() BC=5
BC=5![]() ,
,
在Rt![]() BCA與Rt
BCA與Rt![]() DCE中,
DCE中,
∵∠BAC=∠DEC=30°,
∴tan∠BAC=tan∠DEC,
∴![]() ,
,
∵∠BCA=∠DCE=90°,
∴∠BCA﹣∠DCA=∠DCE﹣∠DCA,
∴∠BCD=∠ACE,
∴![]() BCD∽
BCD∽![]() ACE,
ACE,
∴∠CAE=∠B=60°,![]() ,
,
∴∠DAE=∠DAC+∠CAE=30°+60°=90°,![]() ,
,
∴AE=2![]() ,
,
在Rt![]() ADE中,DE=
ADE中,DE=![]() =
=![]() ,
,
在Rt![]() DCE中,∠DEC=30°,
DCE中,∠DEC=30°,
∴∠EDC=60°,CE=![]() DE=
DE=![]() ,
,
∵∠BAC=∠CEF,∠AFD=∠EFC,
∴![]() AFD∽
AFD∽![]() EFC,
EFC,
∴![]() ,
,
故答案為:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應(yīng)用題系列答案
小學生10分鐘應(yīng)用題系列答案科目:初中數(shù)學 來源: 題型:
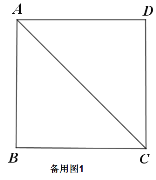
【題目】如圖(1),已知點![]() 在正方形
在正方形![]() 的對角線
的對角線![]() 上,
上,![]() 垂足為點
垂足為點![]() ,垂足為點
,垂足為點![]() .
.
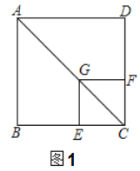
(1)證明與推斷:
![]() 求證:四邊形
求證:四邊形![]() 是正方形;
是正方形;
![]() 推斷:
推斷:![]() 的值為_ _;
的值為_ _;
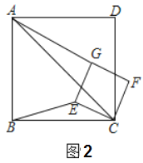
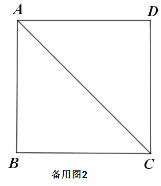
(2)探究與證明:
將正方形![]() 繞點
繞點![]() 順時針方向旋轉(zhuǎn)
順時針方向旋轉(zhuǎn)![]() 角
角![]() ,如圖(2)所示,試探究線段
,如圖(2)所示,試探究線段![]() 與
與![]() 之間的數(shù)量關(guān)系,并說明理由;
之間的數(shù)量關(guān)系,并說明理由;
(3)拓展與運用:
若![]() ,正方形
,正方形![]() 在繞點
在繞點![]() 旋轉(zhuǎn)過程中,當
旋轉(zhuǎn)過程中,當![]() 三點在一條直線上時,則
三點在一條直線上時,則![]() .
.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
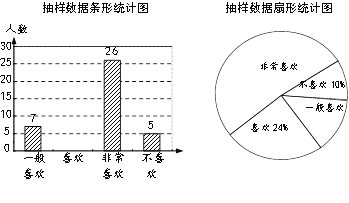
【題目】某校用隨機抽樣的方法在九年級開展了“你是否喜歡網(wǎng)課”的調(diào)查,并將得到的數(shù)據(jù)整理成了以下統(tǒng)計圖(不完整).
(1)此次共調(diào)查了 名學生;
(2)請將條形統(tǒng)計圖補充完整;
(3)若該學校九年級共有300名學生,請你估計其中“非常喜歡”網(wǎng)課的人數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在我市“青山綠水”行動中,某社區(qū)計劃對面積為![]() 的區(qū)域進行綠化,經(jīng)投標由甲、乙兩個工程隊來完成.已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化面積的2倍,如果兩隊各自獨立完成面積為
的區(qū)域進行綠化,經(jīng)投標由甲、乙兩個工程隊來完成.已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化面積的2倍,如果兩隊各自獨立完成面積為![]() 區(qū)域的綠化時,甲隊比乙隊少用6天.
區(qū)域的綠化時,甲隊比乙隊少用6天.
(1)求甲、乙兩工程隊每天各能完成多少面積的綠化;
(2)若甲隊每天綠化費用是1.2萬元,乙隊每天綠化費用為0.5萬元,社區(qū)要使這次綠化的總費用不超過40萬元,則至少應(yīng)安排乙工程隊綠化多少天?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
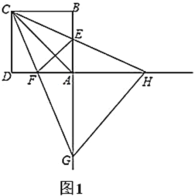
【題目】已知正方形![]() 的邊長為4,點
的邊長為4,點![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上,且
上,且![]() ,直線
,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,直線
,直線![]() 交直線
交直線![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() .
.
(1)如圖1,當![]() 時,求證:
時,求證:![]() 平分
平分![]() ;
;
(2)如圖2,將圖1中的![]() 繞點
繞點![]() 逆時針旋轉(zhuǎn),其他條件不變,(1)的結(jié)論是否成立?說明理由;
逆時針旋轉(zhuǎn),其他條件不變,(1)的結(jié)論是否成立?說明理由;
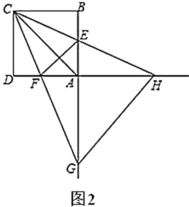
(3)當![]() 是等腰三角形時,直接寫出
是等腰三角形時,直接寫出![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,為了測量建筑物CD、EF的高度,在直線CE上選取觀測點A、B,AC的距離為40米.從A、B測得建筑物的頂部D的仰角分別為51.34°、68.20°,從B、D測得建筑物的頂部F的仰角分別為64.43°、26.57°.
(1)求建筑物CD的高度;
(2)求建筑物EF的高度.
(參考數(shù)據(jù):tan51.34°≈1.25,tan68.20°≈2.5,tan64.43°≈2,tan26.57°≈0.5)

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】網(wǎng)絡(luò)銷售是一種重要的銷售方式.某鄉(xiāng)鎮(zhèn)農(nóng)貿(mào)公司新開設(shè)了一家網(wǎng)店,銷售當?shù)剞r(nóng)產(chǎn)品.其中一種當?shù)靥禺a(chǎn)在網(wǎng)上試銷售,其成本為每千克10元.公司在試銷售期間,調(diào)查發(fā)現(xiàn),每天銷售量y(kg)與銷售單價x(元)滿足如圖所示的函數(shù)關(guān)系(其中![]() ).
).
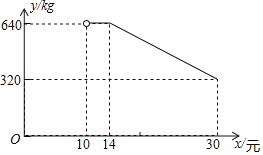
(1)直接寫出y與x之間的函數(shù)關(guān)系式及自變量的取值范圍.
(2)若農(nóng)貿(mào)公司每天銷售該特產(chǎn)的利潤要達到3100元,則銷售單價x應(yīng)定為多少元?
(3)設(shè)每天銷售該特產(chǎn)的利潤為W元,若![]() ,求:銷售單價x為多少元時,每天的銷售利潤最大?最大利潤是多少元?
,求:銷售單價x為多少元時,每天的銷售利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
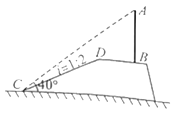
【題目】為積極宣傳國家相關(guān)政策,某村在一山坡的頂端的平地上豎立一塊宣傳牌![]() .小明為測得宣傳牌的高度,他站在山腳
.小明為測得宣傳牌的高度,他站在山腳![]() 處測得宣傳牌的頂端
處測得宣傳牌的頂端![]() 的仰角為
的仰角為![]() ,已知山坡
,已知山坡![]() 的坡度
的坡度![]() ,山坡
,山坡![]() 的長度為
的長度為![]() 米,山坡頂端
米,山坡頂端![]() 與宣傳牌底端
與宣傳牌底端![]() 的水平距離為2米,求宣傳牌的高度
的水平距離為2米,求宣傳牌的高度![]() (精確到1米)
(精確到1米)
(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com