【題目】如圖，已知P為等邊△ABC形內一點，且PA＝3cm，PB＝4 cm，PC＝5 cm，則圖中△PBC的面積為________cm2．
【答案】4
＋3
【解析】
將△BPC繞點B逆時針旋轉60°得到△BKA，可得△KBP為等邊三角形，KP=4，因為AP2+KP2=AK2，可得∠APK=90°，所以∠APB=150°，作BH⊥AP于H，則∠BPH=30°，根據△PBC的面積=△AKB的面積=S△APK+S△BPK-S△APB即可得出△PBC的面積．
解：如圖，將△BPC繞點B逆時針旋轉60°得到△BKA，
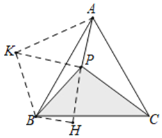
則PB=BK=4，AK=PC=5，∠PBK=60°，
∴△KBP為等邊三角形，
∴∠KPB=60°，KP=4，
∵AP=3，
∴AP2+KP2=AK2，
∴∠APK=90°，
∴∠APB=150°，
作BH⊥AP于H，則∠BPH=30°，
∴BH=
BP=2，
∴△PBC的面積=△AKB的面積=S△APK+S△BPK-S△APB=×3×4+
×42×2×3＝3+4．
故答案為：4+3．
科目：初中數學 來源： 題型：
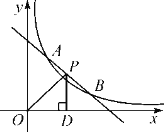
【題目】如圖，一次函數y＝－x＋b與反比例函數y＝
(x＞0)的圖象交于點A(m，3)和B(3，1)．
（1）求一次函數和反比例函數的解析式；
（2）點P(x，y)是直線AB上在第一象限內的一個點，過點P作PD⊥x軸于點D，連接OP，令△POD的面積為S，當S>
時，直接寫出點P橫坐標x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知
、
兩點的坐標分別為
，
，直線
與反比例函數
的圖象相交于點
和點
．
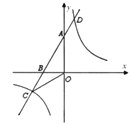
（1）求直線與反比例函數的解析式；
（2）求
的度數；
（3）將
繞點
順時針方向旋轉
角(為銳角)，得到
，當為多少度時
，并求此時線段
的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線
的對稱軸為直線
，與
軸的一個交點坐標為
，其部分圖象如圖所示，有下列結論：①
；②
；③當
時，
隨增大而增大；④拋物線的頂點坐標為
；⑤若方程
兩根為
（
），則
，
.其中正確結論有（ ）
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合與探究
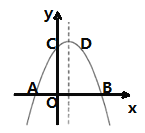
如圖，已知拋物線
與
軸交于
、
兩點，與
軸交于點
，頂點坐標為點
．
（1）求此拋物線的解析式；
（2）點
為拋物線對稱軸上一點，當
最小時，求點坐標；
（3）在第一象限的拋物線上有一點
，當
面積最大時，求點坐標；
（4）在軸下方拋物線上有一點
，
面積為6，請直接寫出點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
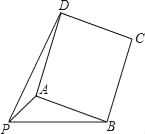
【題目】已知：PA=
，PB＝4，以AB為一邊作正方形ABCD，使P、D兩點落在直線AB的兩側．
(1)如圖，當∠APB＝45°時，求AB及PD的長；
(2)當∠APB變化，且其它條件不變時，求PD的最大值，及相應∠APB的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知直線y＝mx+n（m≠0，且m，n為常數）與雙曲線y＝
（k＜0）在第一象限交于A，B兩點，C，D是該雙曲線另一支上兩點，且A、B、C、D四點按順時針順序排列．
（1）如圖，若m＝﹣
，n＝
，點B的縱坐標為，
①求k的值；
②作線段CD，使CD∥AB且CD＝AB，并簡述作法；
（2）若四邊形ABCD為矩形，A的坐標為（1，5），
①求m，n的值；
②點P（a，b）是雙曲線y＝第一象限上一動點，當S△APC≥24時，則a的取值范圍是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在等邊
中，
，點
在
上，且
，點
是
上一動點，連接
，將線段繞點逆時針旋轉
得到線段
，若要使點
恰好在
上，則
的長為（）．
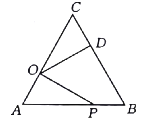
A. 4B. 5C. 6D. 8
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點E、F是邊長為4的正方形ABCD邊AD、AB上的動點，且AF＝DE，BE交CF于點P，在點E、F運動的過程中，PA的最小值為（ ）
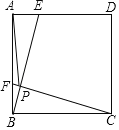
A.2B.2
C.4﹣2D.2
﹣2
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com