
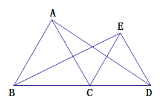
【題目】如圖,點C為線段BD上的一點,△ABC和△CDE是等邊三角形.
(1)求證:AD=BE.
(2)以點C為中心,將△CDE逆時針方向旋轉,旋轉角為ɑ(0°<ɑ<360°).
①當ɑ為多少時DE∥AB?直接寫出結果,不要求證明.
②當BC=6, CD=4時 ,設點E到直線AB的距離為y, 當ɑ為多少時,點E到直線AB的距離最小?求出最小值,并簡潔說明理由.
【答案】(1)證明見解析;(2)120°或300°;(3)![]() ,
,![]() ,證明見解析.
,證明見解析.
【解析】
(1)利用SAS證明△BCE≌△ACD,從而得到結論;
(2)①分兩種情況:當CE旋轉到與CB重合時,DE∥AB;當CE旋轉到BC延長線上時,DE∥AB,從而進行分析即可;
②當點E旋轉到AB邊上的高線上時,到直線AB的距離最小,利用勾股定理可求出,再利用三角形三邊關系及垂線段性質即可證明.
(1)證明:∵△ABC和△CDE是等邊三角形,
∴BC=AC,CE=CD,∠BCA=∠ECD=60°,
∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,
∴△BCE≌△ACD(SAS)
∴AD=BE;
(2)解:①情況一:當![]() 時,DE∥AB,證明如下:
時,DE∥AB,證明如下:
當![]() 時,此時CE旋轉到與CB重合,
時,此時CE旋轉到與CB重合,
∵△ABC和△CDE是等邊三角形,
∴∠DEC=∠ABC=60°,
∴DE∥AB(同位角相等,兩直線平行);
情況二:當![]() 時,DE∥AB,證明如下:
時,DE∥AB,證明如下:
當![]() 時,此時CE旋轉到BC延長線上,
時,此時CE旋轉到BC延長線上,
∵△ABC和△CDE是等邊三角形,
∴∠DEC=∠ABC=60°,
∴DE∥AB(內錯角相等,兩直線平行);
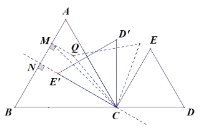
②如圖,當![]() 時,點E旋轉至點E',此時點E'到AB的距離最短,NC⊥AB,
時,點E旋轉至點E',此時點E'到AB的距離最短,NC⊥AB,
在Rt△ANC中,AC=6,AN=![]() ,
,
∴NC=![]() ,
,
∴![]() ,
,
如圖,Q為E旋轉任意角度后所對應的點,根據三角形三邊關系可知,CQ+QM![]() MC,
MC,
根據垂線段最短可知,CE'+NE'![]() MC
MC![]() CQ+QM,當點Q與點E'重合時取等號,即:NE'≤QM,
CQ+QM,當點Q與點E'重合時取等號,即:NE'≤QM,
所以當![]() 時,點E到直線AB的距離最小,最小值為
時,點E到直線AB的距離最小,最小值為![]() .
.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源: 題型:
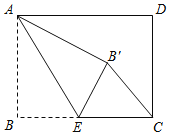
【題目】如圖,在矩形ABCD中,AB=5,BC=12,點E是BC邊上一點,連接AE,將△ABE沿AE折疊,使點B落在點B′處.當△CEB′為直角三角形時,![]() _____.
_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】箱子里有4瓶牛奶,其中有一瓶是過期的.現從這4瓶牛奶中不放回地任意抽取2瓶.
(1)請用樹狀圖或列表法把上述所有等可能的結果表示出來;
(2)求抽出的2瓶牛奶中恰好抽到過期牛奶的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=-2,與x軸的一個交點在(-3,0)和(-4,0)之間,其部分圖象如圖所示,則下列結論:①3a-c<0;② abc<0; ③點![]() ,
,![]() ,
,![]() 是該拋物線上的點,則
是該拋物線上的點,則![]() ; ④4a-2b≥at2+bt(t為實數);正確的個數有()個
; ④4a-2b≥at2+bt(t為實數);正確的個數有()個
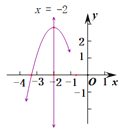
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=8cm,BC=16cm,點P從點A開始沿邊AB向點B以2cm/s的速度移動,點Q從點B開始沿邊BC向點C以4cm/s的速度移動,如果點P、Q分別從點A、B同時出發,經幾秒鐘△PBQ與△ABC相似?試說明理由.
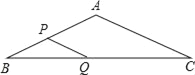
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行于x軸的直線AC分別交拋物線![]() 與
與![]() 于B、C兩點,過點C作y軸的平行線交y1于點D,直線DE∥AC,交y2于點E,則DE:BC=______.
于B、C兩點,過點C作y軸的平行線交y1于點D,直線DE∥AC,交y2于點E,則DE:BC=______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() .點
.點![]() 是
是![]() 中點,點
中點,點![]() 為邊
為邊![]() 上一點,連接
上一點,連接![]() ,以
,以![]() 為邊在
為邊在![]() 的左側作等邊三角形
的左側作等邊三角形![]() ,連接
,連接![]() .
.
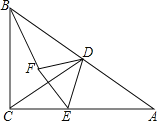
(1)![]() 的形狀為______;
的形狀為______;
(2)隨著點![]() 位置的變化,
位置的變化,![]() 的度數是否變化?并結合圖說明你的理由;
的度數是否變化?并結合圖說明你的理由;
(3)當點![]() 落在邊
落在邊![]() 上時,若
上時,若![]() ,請直接寫出
,請直接寫出![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com