
【題目】在“全國愛眼日”這天,某校課題小組為了了解本校![]() 名學生的視力情況,隨機抽查了部分學生的視力,并將調查的數據整理后繪制成如下的頻率分布表和頻數分布直方圖(均不完整).
名學生的視力情況,隨機抽查了部分學生的視力,并將調查的數據整理后繪制成如下的頻率分布表和頻數分布直方圖(均不完整).
組別 | 視力 | 頻率 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
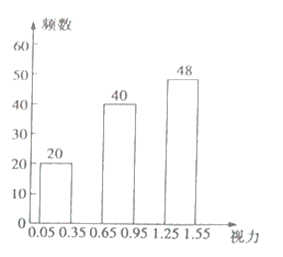
根據以上信息解答下列問題:
![]() 填空:
填空:![]() ______ _,并將頻數分布直方圖補充完整;
______ _,并將頻數分布直方圖補充完整;
![]() 若將統計結果繪制成扇形統計圖,則第
若將統計結果繪制成扇形統計圖,則第![]() 組所在扇形的圓心角度數為 ;
組所在扇形的圓心角度數為 ;
![]() 課題小組調查發現,每組中過度使用電子產品而造成視力下降的學生的比重如下表:
課題小組調查發現,每組中過度使用電子產品而造成視力下降的學生的比重如下表:
視力 |
|
|
|
|
|
比重 |
|
|
|
|
|
根據調查結果估計該校有多少名學生的視力下降是由于過度使用電子產品.
【答案】(1)0.18,補全圖形見解析;(2)86.4°;(3)215名
【解析】
(1)根據頻率值和為1,利用總調查人數等于所占人數除以所占百分比計算即可得到答案;
(2)根據總度數為360°,乘以所占比例即可得到答案;
(3)根據權重的計算公式,即可得到答案
(1)![]() 根據頻率之和為1,結合表格的信息得:
根據頻率之和為1,結合表格的信息得:
![]() ,
,
總抽查人數為:![]() (人),
(人),
故視力在![]() 的人數為:
的人數為:![]() (人),
(人),
視力在![]() 的人數為:200-20-36-40-48=56(人),
的人數為:200-20-36-40-48=56(人),
補全頻數分布直方圖如圖所示.
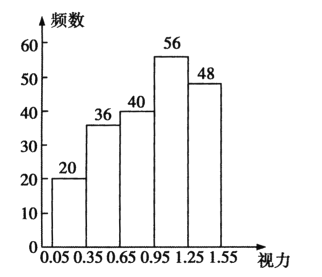
(2)第五組人數的頻率是0.24,
∵總扇形度數為360°,
故第五組所占圓心角度數為:
![]() ;
;
![]() 調查的學生中,過度使用電子產品而造成視力下降的學生人數為:
調查的學生中,過度使用電子產品而造成視力下降的學生人數為:![]() ,
,
因為學校總人數為1000,故估計該校因過度使用電子產品而造成視力下降的學生有:
![]() (名).
(名).


 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:
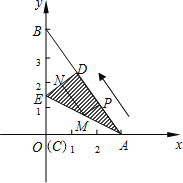
【題目】如圖所示,Rt△ABC是一張放在平面直角坐標系中的紙片,點C與原點O重合,點A在x軸的正半軸上,點B在y軸的正半軸上,已知OA=3,OB=4.將紙片的直角部分翻折,使點C落在AB邊上,記為D點,AE為折痕,E在y軸上.
(1)在下圖所示的直角坐標系中,求E點的坐標及AE的長.
(2)線段AD上有一動點P(不與A、D重合)自A點沿AD方向以每秒1個單位長度向D點作勻速運動,設運動時間為t秒(0<t<3),過P點作PM∥DE交AE于M點,過點M作MN∥AD交DE于N點,求四邊形PMND的面積S與時間t之間的函數關系式,當t取何值時,S有最大值?最大值是多少?
(3)當t(0<t<3)為何值時,A、D、M三點構成等腰三角形?并求出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了促進學生多樣化發展,某校組織開展了社團活動,分別設置了體育類、藝術類、文學類及其它類社團(要求人人參與社團,每人只能選擇一項).為了解學生喜愛哪種社團活動,學校做了一次抽樣調查.根據收集到的數據,繪制成如下兩幅不完整的統計圖,請根據圖中提供的信息,完成下列問題:

(1)此次共調查了多少人?
(2)求文學社團在扇形統計圖中所占圓心角的度數;
(3)請將條形統計圖補充完整;
(4)若該校有1500名學生,請估計喜歡體育類社團的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】籃球運動是全世界最流行的運動之一,近年流行于青少年之間的“3對3”籃球將登上2020年奧運會賽場,為備戰某市中學生“3對3”籃球聯賽,某校甲、乙、丙三位同學作為“兄弟戰隊”的主力隊員進行籃球傳球訓練,籃球由一個人隨機傳給另一個人,且每位傳球人傳球給其余兩人的機會是均等的,現在由甲開始傳球.
(1)求甲第一次傳球給乙的概率;
(2)三次傳球后,籃球在誰手中的可能性大?請利用樹狀圖說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】利用如圖1的二維碼可以進行身份識別.某校建立了一個身份識別系統,圖2是某個學生的識別圖案,黑色小正方形表示1,白色小正方形表示0.將第一行數字從左到右依次記為![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以轉換為該生所在班級序號,其序號為
,那么可以轉換為該生所在班級序號,其序號為![]() .如圖2第一行數字從左到右依次為0,1,0,1,序號為
.如圖2第一行數字從左到右依次為0,1,0,1,序號為![]() ,表示該生為5班學生.表示6班學生的識別圖案是( )
,表示該生為5班學生.表示6班學生的識別圖案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校八年級舉行英語演講比賽,準備用1200元錢(全部用完)購買A,B兩種筆記本作為獎品,已知A,B兩種每本分別為12元和20元,設購入A種x本,B種y本.
(1)求y關于x的函數表達式.
(2)若購進A種的數量不少于B種的數量.
①求至少購進A種多少本?
②根據①的購買,發現B種太多,在費用不變的情況下把一部分B種調換成另一種C,調換后C種的數量多于B種的數量,已知C種每本8元,則調換后C種至少有______本(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
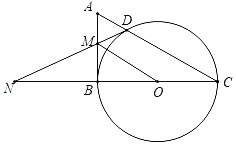
【題目】如圖,在Rt△ABC中,以BC為直徑的⊙O交AC于點D,過點D作⊙O的切線交AB于點M,交CB延長線于點N,連接OM,OC=1.
(1)求證:AM=MD;
(2)填空:
①若DN![]() ,則△ABC的面積為 ;
,則△ABC的面積為 ;
②當四邊形COMD為平行四邊形時,∠C的度數為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
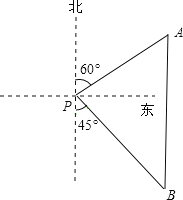
【題目】如圖,一艘漁船位于海洋觀測站P的北偏東60°方向,漁船在A處與海洋觀測站P的距離為60海里,它沿正南方向航行一段時間后,到達位于海洋觀測站P的南偏東45°方向上的B處.求此時漁船所在的B處與海洋觀測站P的距離(結果保留根號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com