
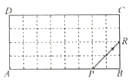
【題目】如圖,在矩形![]() 中,
中,![]() ,一發(fā)光電子開始置于
,一發(fā)光電子開始置于![]() 邊的點(diǎn)
邊的點(diǎn)![]() 處,并設(shè)定此時為發(fā)光電子第一次與矩形的邊碰撞,將發(fā)光電子沿著
處,并設(shè)定此時為發(fā)光電子第一次與矩形的邊碰撞,將發(fā)光電子沿著![]() 方向發(fā)射,碰撞到矩形的邊時均反射,每次反射的反射角和入射角都等于
方向發(fā)射,碰撞到矩形的邊時均反射,每次反射的反射角和入射角都等于![]() ,當(dāng)發(fā)光電子與矩形的邊碰撞2020次后,它與
,當(dāng)發(fā)光電子與矩形的邊碰撞2020次后,它與![]() 邊的碰撞次數(shù)是__________.
邊的碰撞次數(shù)是__________.
【答案】674
【解析】
根據(jù)反射角與入射角的定義可以在格點(diǎn)中作出圖形,可以發(fā)現(xiàn),在經(jīng)過6次反射后,發(fā)光電子回到起始的位置,即可求解.
解:如圖,設(shè)A點(diǎn)坐標(biāo)為(0,0),
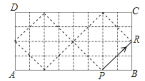
根據(jù)圖形可以得到:每6次反彈為一個循環(huán)組依次循環(huán),經(jīng)過6次反彈后動點(diǎn)回到出發(fā)點(diǎn)(6,0),且每次循環(huán)它與AB邊的碰撞有2次,
∵2020÷6=336…4,
當(dāng)點(diǎn)P第2020次碰到矩形的邊時為第337個循環(huán)組的第4次反彈,點(diǎn)P的坐標(biāo)為(2,0),
∴它與AB邊的碰撞次數(shù)是=336×2+2=674次;
故答案為674.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如果一個圓上所有的點(diǎn)都在一個角的內(nèi)部或邊上,那么稱這個圓為該角的角內(nèi)圓.特別地,當(dāng)這個圓與角的至少一邊相切時,稱這個圓為該角的角內(nèi)相切圓.在平面直角坐標(biāo)系![]() 中,點(diǎn)
中,點(diǎn)![]() ,
,![]() 分別在
分別在![]() 軸的正半軸和
軸的正半軸和![]() 軸的正半軸上.
軸的正半軸上.
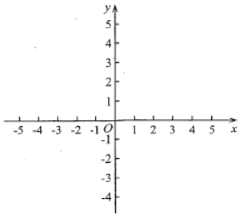
(1)分別以點(diǎn)![]() ,
,![]() ,
,![]() 為圓心,
為圓心,![]() 為半徑作圓,得到
為半徑作圓,得到![]() ,
,![]() 和
和![]() ,其中是
,其中是![]() 的角內(nèi)圓的是_______;
的角內(nèi)圓的是_______;
(2)如果以點(diǎn)![]() 為圓心,以
為圓心,以![]() 為半徑的
為半徑的![]() 為
為![]() 的角內(nèi)圓,且與一次函數(shù)圖像
的角內(nèi)圓,且與一次函數(shù)圖像![]() 有公共點(diǎn),求
有公共點(diǎn),求![]() 的取值范圍;
的取值范圍;
(3)點(diǎn)![]() 在第一象限內(nèi),如果存在一個半徑為
在第一象限內(nèi),如果存在一個半徑為![]() 且過點(diǎn)
且過點(diǎn)![]() 的圓為∠EOM的角內(nèi)相切圓,直接寫出∠EOM的取值范圍.
的圓為∠EOM的角內(nèi)相切圓,直接寫出∠EOM的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為全面貫徹黨的教育方針和落實(shí)陽光體育運(yùn)動,提高青少年學(xué)生身體健康水平和體育運(yùn)動水平,某校準(zhǔn)備購買一批籃球,甲、乙兩家商店的標(biāo)價都是每個![]() 元,兩家商店推出不同的優(yōu)惠方式如下表:
元,兩家商店推出不同的優(yōu)惠方式如下表:
商店 | 優(yōu)惠方式 |
甲 | 購買數(shù)量不超過 |
乙 | 按照標(biāo)價的八折銷售 |
(1)設(shè)該學(xué)校購買![]() 個籃球,在甲商店購買花費(fèi)
個籃球,在甲商店購買花費(fèi)![]() 元,在商店購買花費(fèi)
元,在商店購買花費(fèi)![]() 元,請分別求出
元,請分別求出![]() 、
、![]() 與
與![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(2)若學(xué)校需購買![]() 個籃球,請你通過計(jì)算進(jìn)行對比,選擇哪家商店更省錢?
個籃球,請你通過計(jì)算進(jìn)行對比,選擇哪家商店更省錢?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某班班長統(tǒng)計(jì)去年18月“書香校園”活動中全班同學(xué)的課外閱讀數(shù)量(單位:本),繪制了如圖折線統(tǒng)計(jì)圖,下列說法正確的是( )
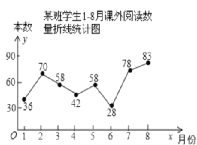
A. 每月閱讀數(shù)量的平均數(shù)是50
B. 眾數(shù)是42
C. 中位數(shù)是58
D. 每月閱讀數(shù)量超過40的有4個月
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
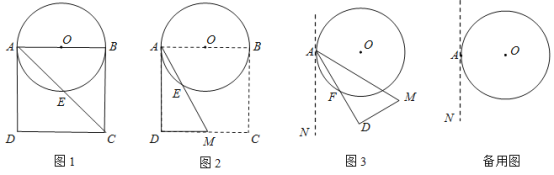
【題目】如圖![]() , 以邊長為
, 以邊長為![]() 的正方形紙片
的正方形紙片![]() 的邊
的邊![]() 為直徑做
為直徑做![]() , 交對角線
, 交對角線![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)線段![]()
(2) 如圖![]() , 以點(diǎn)
, 以點(diǎn)![]() 為端點(diǎn)作
為端點(diǎn)作![]() , 交
, 交![]() 于點(diǎn)
于點(diǎn)![]() , 沿
, 沿![]() 將四邊形
將四邊形![]() 剪掉, 使
剪掉, 使![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)(如圖
逆時針旋轉(zhuǎn)(如圖![]() ),設(shè)旋轉(zhuǎn)角為
),設(shè)旋轉(zhuǎn)角為![]() , 旋轉(zhuǎn)過程中
, 旋轉(zhuǎn)過程中![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() .
.
①當(dāng)![]() 時,請求出線段
時,請求出線段![]() 的長;
的長;
②當(dāng)![]() 時,求出線段
時,求出線段![]() 的長;判斷此時與
的長;判斷此時與![]() 的位置關(guān)系,并說明理由;
的位置關(guān)系,并說明理由;
③當(dāng)![]() 時,
時,![]() 與
與![]() 相切.
相切.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
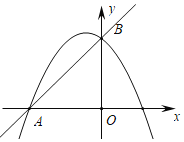
【題目】在平面直角坐標(biāo)系中,直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,拋物線
,拋物線![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() 、
、![]() .
.
(1)求![]() 、
、![]() 滿足的關(guān)系式及
滿足的關(guān)系式及![]() 的值.
的值.
(2)當(dāng)![]() 時,若
時,若![]() 的函數(shù)值隨
的函數(shù)值隨![]() 的增大而增大,求
的增大而增大,求![]() 的取值范圍.
的取值范圍.
(3)如圖,當(dāng)![]() 時,在拋物線上是否存在點(diǎn)
時,在拋物線上是否存在點(diǎn)![]() ,使
,使![]() 的面積為1?若存在,請求出符合條件的所有點(diǎn)
的面積為1?若存在,請求出符合條件的所有點(diǎn)![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,菱形![]() 的兩條對角線相交于點(diǎn)
的兩條對角線相交于點(diǎn)![]() 軸,垂足為點(diǎn)
軸,垂足為點(diǎn)![]() 正比例函數(shù)
正比例函數(shù)![]() 的圖像與反比例函數(shù)
的圖像與反比例函數(shù)![]() 的圖像相交于
的圖像相交于![]() 兩點(diǎn).
兩點(diǎn).

(1)求正比例函數(shù)和反比例函數(shù)的解析式;
(2)求點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
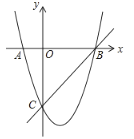
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)![]() 為坐標(biāo)原點(diǎn).拋物線
為坐標(biāo)原點(diǎn).拋物線![]() 交
交![]() 軸于
軸于![]() 、
、![]() 兩點(diǎn),交
兩點(diǎn),交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,直線
,直線![]() 經(jīng)過
經(jīng)過![]() 、
、![]() 兩點(diǎn).
兩點(diǎn).
(1)求拋物線的解析式;
(2)過點(diǎn)![]() 作直線
作直線![]() 軸交拋物線于另一點(diǎn)
軸交拋物線于另一點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,連接
,連接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,頂點(diǎn)坐標(biāo)
,頂點(diǎn)坐標(biāo)![]() ,與
,與![]() 軸的交點(diǎn)在
軸的交點(diǎn)在![]() ,
,![]() 之間(包含端點(diǎn)),則下列結(jié)論:①
之間(包含端點(diǎn)),則下列結(jié)論:①![]() ;②
;②![]() ;③對于任意實(shí)數(shù)
;③對于任意實(shí)數(shù)![]() ,
,![]() 總成立;④關(guān)于
總成立;④關(guān)于![]() 的方程
的方程![]() 有兩個不相等的實(shí)數(shù)根.其中結(jié)論正確的個數(shù)為( )
有兩個不相等的實(shí)數(shù)根.其中結(jié)論正確的個數(shù)為( )
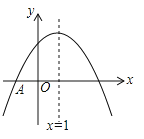
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com