
【題目】小穎在完成一項“社會調(diào)查”作業(yè)時,需要調(diào)查城市送餐人員的收入情況,他了解到勞務(wù)公司為了鼓勵送餐員的工作積極性,實行“月總收入![]() 基本工資(固定)
基本工資(固定)![]() 送餐單數(shù)獎勵”的方法計算薪資,調(diào)查中獲得如下信息:
送餐單數(shù)獎勵”的方法計算薪資,調(diào)查中獲得如下信息:
送餐員 | 小李 | 小楊 |
月送餐單數(shù)/單 | 292 | 273 |
月總收入/元 | 3384 | 3346 |
送餐每單獎勵![]() 元,送餐員月基本工資為
元,送餐員月基本工資為![]() 元;
元;
(1)求a、b的值;
(2)若月送餐單數(shù)超過300單時,超過部分每單的獎金增加1元.假設(shè)月送餐單數(shù)為![]() 單,月總收入為
單,月總收入為![]() 元,請寫出
元,請寫出![]() 與
與![]() 的函數(shù)關(guān)系式,若送餐員小李計劃月收入不低于5200元,那么他每月至少要送多少單?
的函數(shù)關(guān)系式,若送餐員小李計劃月收入不低于5200元,那么他每月至少要送多少單?
【答案】(1)![]() ;(2)至少要送900單.
;(2)至少要送900單.
【解析】
(1)利用月總收入![]() 基本工資(固定)
基本工資(固定)![]() 送餐單數(shù)獎勵建立方程組求解;
送餐單數(shù)獎勵建立方程組求解;
(2)與![]() 的函數(shù)關(guān)系式需要分情況討論,當(dāng)
的函數(shù)關(guān)系式需要分情況討論,當(dāng)![]() 時,用基本工資加上每單a元的獎勵即為月收入,當(dāng)
時,用基本工資加上每單a元的獎勵即為月收入,當(dāng)![]() 時,用基本工資加上300單每單a元的獎勵,再加超過300單的部分每單(a+1)元的獎勵即為收入;當(dāng)
時,用基本工資加上300單每單a元的獎勵,再加超過300單的部分每單(a+1)元的獎勵即為收入;當(dāng)![]() 時,建立不等式求解.
時,建立不等式求解.
(1)由題意得:
![]()
解得![]() .
.
(2)當(dāng)![]() 時,
時,
![]() ,
,
當(dāng)![]() 時,
時,
![]()
∴y與x的函數(shù)關(guān)系式為: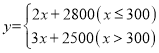
當(dāng)x=300時,![]()
∴月收入要不低于5200元,送餐單數(shù)必須大于300
則![]()
解得![]()
∴小李計劃月收入不低于5200元,那么他每月至少要送900單.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知正方形ABCD的邊長為3,E、F分別是AB、BC邊上的點,且∠EDF=45°,將△DAE繞點D逆時針旋轉(zhuǎn)90°,得到△DCM.若AE=1,則FM的長為 .

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,為了躲避臺風(fēng),一輪船一直由西向東航行,上午![]() 點,在
點,在![]() 處測得小島
處測得小島![]() 的方向是北偏東
的方向是北偏東![]() ,以每小時
,以每小時![]() 海里的速度繼續(xù)向東航行,中午
海里的速度繼續(xù)向東航行,中午![]() 點到達(dá)
點到達(dá)![]() 處,并測得小島
處,并測得小島![]() 的方向是北偏東
的方向是北偏東![]() ,若小島周圍
,若小島周圍![]() 海里內(nèi)有暗礁,問該輪船是否能一直向東航行?
海里內(nèi)有暗礁,問該輪船是否能一直向東航行?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,以AB為直徑的
,以AB為直徑的![]() 分別與
分別與![]() 交于點
交于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() .
.
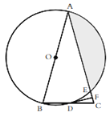
(1)求證:DF是![]() 的切線;
的切線;
(2)若![]() 的半徑為3,
的半徑為3,![]() ,求陰影部分的面積;
,求陰影部分的面積;
(3)求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知直線y=kx+b與拋物線y=ax2(a>0)相交于A、B兩點(點A在點B的左側(cè)),與y軸正半軸相交于點C,過點A作AD⊥x軸,垂足為D.
(1)若∠AOB=60°,AB∥x軸,AB=2,求a的值;
(2)若∠AOB=90°,點A的橫坐標(biāo)為﹣4,AC=4BC,求點B的坐標(biāo);
(3)延長AD、BO相交于點E,求證:DE=CO.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列命題的逆命題是真命題的是( )
A.兩直線平行,同位角相等
B.等邊三角形是銳角三角形
C.如果兩個實數(shù)是正數(shù),那么它們的積是正數(shù)
D.全等三角形的對應(yīng)角相等
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
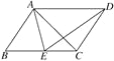
【題目】如圖,在ABCD中,E為BC邊上一點,且AB=AE,若AE平分∠DAB,∠EAC=25°,則∠AED的度數(shù)是______度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
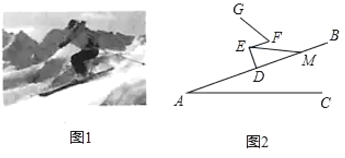
【題目】圖1,圖2分別是一滑雪運動員在滑雪過程中某一時刻的實物圖與示意圖,已知運動員的小腿![]() 與斜坡
與斜坡![]() 垂直,大腿
垂直,大腿![]() 與斜坡
與斜坡![]() 平行,且
平行,且![]() 三點共線,若雪仗
三點共線,若雪仗![]() 長為
長為![]() ,
,![]() ,
,![]() ,求此刻運動員頭部
,求此刻運動員頭部![]() 到斜坡
到斜坡![]() 的高度
的高度![]() (精確到
(精確到![]() )(參考數(shù)據(jù):
)(參考數(shù)據(jù):![]() )
)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
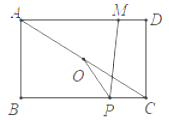
【題目】如圖,在矩形ABCD中,AB=4,AD=5,連接AC,O是AC的中點,M是AD上一點,且MD=1,P是BC上一動點,則PM﹣PO的最大值為_____.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com