
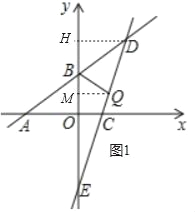
【題目】已知:如圖,一次函數![]() 的圖象分別與x軸、y軸相交于點A、B,且與經過點C(2,0)的一次函數y=kx+b的圖象相交于點D,點D的橫坐標為4,直線CD與y軸相交于點E.
的圖象分別與x軸、y軸相交于點A、B,且與經過點C(2,0)的一次函數y=kx+b的圖象相交于點D,點D的橫坐標為4,直線CD與y軸相交于點E.
(1)直線CD的函數表達式為 ;(直接寫出結果)
(2)點Q為線段DE上的一個動點,連接BQ.
①若直線BQ將△BDE的面積分為1:2兩部分,試求點Q的坐標;
②將△BQD沿著直線BQ翻折,使得點D恰好落在直線AB下方的坐標軸上,請直接寫出點Q的坐標: .

【答案】(1)y=3x﹣6;(2)①(![]() ,﹣2)或(
,﹣2)或(![]() ,2);②存在,點Q的坐標為(3,3)或(
,2);②存在,點Q的坐標為(3,3)或(![]() ,
,![]() ).
).
【解析】
(1)求出C、D兩點坐標即可解決問題;
(2)①分兩種情形S△BEQ=![]() S△BDE或S△BEQ=
S△BDE或S△BEQ=![]() S△BDE分別構建方程即可;
S△BDE分別構建方程即可;
②分兩種情形:當點D落在x正半軸上(記為點D1)時,如圖2中;當點D落在y負半軸上(記為點D2)時,如圖3中;分別求解即可.
解:(1)由題意:D(4,6),C(2,0),
設直線CD的解析式為y=kx+b,
則有![]() ,
,
解得![]() ,
,
∴直線CD的解析式為y=3x﹣6,
故答案為:y=3x﹣6;
(2)①∵直線BQ將△BDE的面積分為1:2兩部分,
∴S△BEQ=![]() S△BDE或S△BEQ=
S△BDE或S△BEQ=![]() S△BDE,
S△BDE,
在y=![]() x+3中,當x=0時,y=3;當x=4時,y=6,
x+3中,當x=0時,y=3;當x=4時,y=6,
∴B(0,3),D(4,6).
在y=3x﹣6中,當x=0時,y=﹣6,
∴E(0,﹣6),
∴BE=9,
如圖1中,過點D作DH⊥y軸于點H,則DH=4,
∴S△BDE=![]() BEDH=
BEDH=![]() ×9×4=18,
×9×4=18,
∴S△BEQ=![]() ×18=6或S△BEQ=
×18=6或S△BEQ=![]() ×18=12,
×18=12,
設Q(t,3t﹣6),由題意知t>0,
過點Q作QM⊥y軸于點M,則QM=t,
∴![]() ×9×t=6或
×9×t=6或![]() ×9×t=12,
×9×t=12,
解得t=![]() 或
或![]() ,
,
當t=![]() 時,3t﹣6=﹣2,
時,3t﹣6=﹣2,
當t=![]() 時3t﹣6=2,
時3t﹣6=2,
∴Q的坐標為(![]() ,﹣2)或(
,﹣2)或(![]() ,2);
,2);
②當點D落在x正半軸上(記為點D1)時,如圖2中,
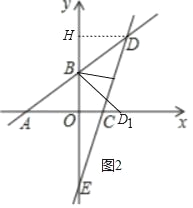
由(2)知B(0,3),D(4,6),
∴BH=BO=3,
由翻折得BD=BD1,
在△Rt△DHB和Rt△D1OB中,
![]() ,
,
∴Rt△DHB≌Rt△D1OB(HL),
∴∠DBH=∠D1BO,
由翻折得∠DBQ=∠D1BQ,
∴∠HBQ=∠OBQ=90°,
∴BQ∥x軸,
∴點Q的縱坐標為3,
在y=3x﹣6中,當y=3時,x=3,
∴Q(3,3);
當點D落在y負半軸上(記為點D2)時,如圖3中,
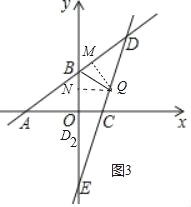
過點Q作QM⊥BD,QN⊥OB,垂足分別為點M、N,
由翻折得∠DBQ=∠D2BQ,
∴QM=QN,
由(2)知S△BDE=18,即S△BQD+S△BQE=18,
∴![]() BDQM+
BDQM+![]() BEQN=18,
BEQN=18,
由兩點之間的距離公式,得BD=![]() =5,
=5,
∴![]() ×5QN+
×5QN+![]() ×9QN=18,
×9QN=18,
解得QN=![]() ,
,
∴點Q的橫坐標為![]() ,
,
在y=3x﹣6中,當x=時,y=
![]() ,
,
∴Q(![]() ,
,![]() ).
).
綜合知,點Q的坐標為(3,3)或(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
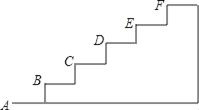
【題目】如圖是某臺階的一部分,如果A點的坐標為(0,0),B點的坐標為(1,1),
(1)請建立適當的直角坐標系,并寫出其余各點的坐標;
(2)如果臺階有10級,請你求出該臺階的長度和高度;
(3)若這10級臺階的寬度都是2m,單位長度為1m,現要將這些臺階鋪上地毯,需要多少平方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場計劃購進![]() 、
、![]() 兩種新型節能臺燈共
兩種新型節能臺燈共![]() 盞,這兩種臺燈的進價、售價如表所示:
盞,這兩種臺燈的進價、售價如表所示:

(![]() )若商場預計進貨款為
)若商場預計進貨款為![]() 元,則這兩種臺燈各購進多少盞?
元,則這兩種臺燈各購進多少盞?
(![]() )若商場規定
)若商場規定![]() 型臺燈的進貨數量不超過
型臺燈的進貨數量不超過![]() 型臺燈數量的
型臺燈數量的![]() 倍,應怎樣進貨才能使商場在銷售完這批臺燈時獲利最多?此時利潤為多少元?
倍,應怎樣進貨才能使商場在銷售完這批臺燈時獲利最多?此時利潤為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校開展課外體育活動,決定開展:籃球、乒乓球、踢毽子、跑步四種活動項目.為了解學生最喜歡哪一種活動項目(每人只選取一種).隨機抽取了部分學生進行調查,并將調查結果繪成如下統計圖,請你結合圖中信息解答下列問題.
(1)樣本中最喜歡籃球項目的人數所占的百分比為 ,其所在扇形統計圖中對應的圓心角度數是 度;
(2)請把條形統計圖補充完整;
(3)若該校有學生1000人,請根據樣本估計全校最喜歡踢毽子的學生人數約是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
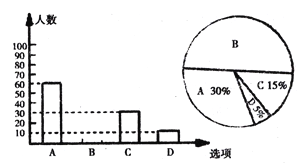
【題目】為了解學生參加體育活動的情況,學校對學生進行隨機抽樣調查,其中一個問題是“你平均每天參加體育活動的時間是多少?”共有4個選題.
A.1.5小時以上 B.1~1.5小時 C.0.5~1小時 D.0.5小時以下
請你根據統計圖提供的信息,解答以下問題:
(1)本次一共調查了多少名學生?
(2)將條形統計圖選項B補充完整;
(3)若該校有3000名學生,你估計全校可能有多少名學生平均每天參加體育活動的時間在0.5小時以下?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AB為⊙O的直徑,⊙O與DC相切于點E,與AD相交于點F,已知AB=12,∠C=60°,則 ![]() 的長為( )
的長為( ) 
A.![]()
B.![]()
C.π
D.2π
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公園的門票每張10元,為了吸引更多的游客,該公園管理除保留原來的售票方法外,還推出了一種“購買年卡”的優惠方法,年卡分為A、B、C三種:A卡每張120元,持卡進入不用再買門票;B卡每張60元,持卡進入公園需要再買門票,每張2元;C卡每張30元,持票進入公園時,購買每張4元的門票.
(1)如果你只選擇一種購買門票的方式,并且你計劃在一年中用100元花在去該公園玩的門票上,請問哪種購票方式可使你進入該公園的次數最多?
(2)求一年中進入該公園至少多少次,購買A類年票比較合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
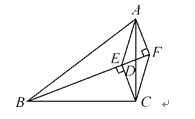
【題目】如圖所示,BD是△ABC的中線,CE⊥BD于點E,AF⊥BD,交BD的延長線于點F.
(1)試探索BE,BF和BD三者之間的數量關系,并加以證明;
(2)連接AE,CF,求證:AE∥CF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某晚報“百姓熱線”一周內接到熱線電話的統計圖,其中有關環境保護問題的電話最多,共70個,請回答下列問題:

(1)本周“百姓熱線”共接到熱線電話多少個?
(2)有關道路交通問題的電話多少個?
(3)計算其他各類電話的個數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com