Question

【題目】如圖，菱形ABCD的邊長為2，∠DAB=60°，E為BC的中點，在對角線AC上存在一點P，使△PBE的周長最小，則△PBE的周長的最小值為 ．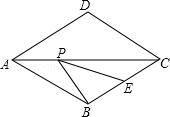

Answer 1

【答案】
+1
【解析】解：連結DE．
∵BE的長度固定，
∴要使△PBE的周長最小只需要PB+PE的長度最小即可，
∵四邊形ABCD是菱形，
∴AC與BD互相垂直平分，
∴P′D=P′B，
∴PB+PE的最小長度為DE的長，
∵菱形ABCD的邊長為2，E為BC的中點，∠DAB=60°，
∴△BCD是等邊三角形，
又∵菱形ABCD的邊長為2，
∴BD=2，BE=1，DE= ，
∴△PBE的最小周長=DE+BE= +1，
故答案為： +1．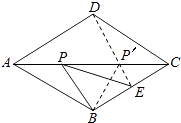

連接BD，與AC的交點即為使△PBE的周長最小的點P；由菱形的性質得出∠BPC=90°，由直角三角形斜邊上的中線性質得出PE=BE，證明△PBE是等邊三角形，得出PB=BE=PE=1，即可得出結果．