
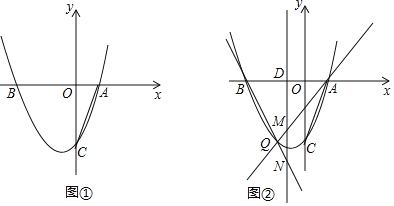
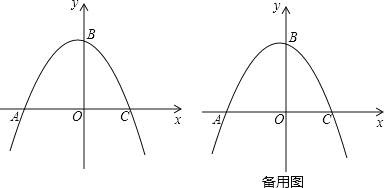
【題目】如圖,拋物線y=x2+bx+c交x軸于A、B兩點,其中點A坐標為(1,0),與y軸交于點C(0,﹣3).
(1)求拋物線的函數表達式;
(2)如圖①,連接AC,點P在拋物線上,且滿足∠PAB=2∠ACO.求點P的坐標;
(3)如圖②,點Q為x軸下方拋物線上任意一點,點D是拋物線對稱軸與x軸的交點,直線AQ、BQ分別交拋物線的對稱軸于點M、N.請問DM+DN是否為定值?如果是,請求出這個定值;如果不是,請說明理由.
【答案】(1)拋物線的函數表達式為y=x2+2x﹣3;(2)點P的坐標為![]() ,
,![]() 或
或![]() ,
,![]() ;(3)為定值8.
;(3)為定值8.
【解析】
(1)把點![]() 、
、![]() 坐標代入拋物線解析式即求得
坐標代入拋物線解析式即求得![]() 、
、![]() 的值.
的值.
(2)點![]() 可以在
可以在![]() 軸上方或下方,需分類討論.①若點
軸上方或下方,需分類討論.①若點![]() 在
在![]() 軸下方,延長
軸下方,延長![]() 到
到![]() ,使
,使![]() 構造等腰
構造等腰![]() ,作
,作![]() 中點
中點![]() ,即有
,即有![]() ,利用
,利用![]() 的三角函數值,求
的三角函數值,求![]() 、
、![]() 的長,進而求得
的長,進而求得![]() 的坐標,求得直線
的坐標,求得直線![]() 的解析式后與拋物線解析式聯立,即求出點
的解析式后與拋物線解析式聯立,即求出點![]() 坐標.②若點
坐標.②若點![]() 在
在![]() 軸上方,根據對稱性,
軸上方,根據對稱性,![]() 一定經過點
一定經過點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() ,求得直線
,求得直線![]() 的解析式后與拋物線解析式聯立,即求出點
的解析式后與拋物線解析式聯立,即求出點![]() 坐標.
坐標.
(3)設點![]() 橫坐標為
橫坐標為![]() ,用
,用![]() 表示直線
表示直線![]() 、
、![]() 的解析式,把
的解析式,把![]() 分別代入即求得點
分別代入即求得點![]() 、
、![]() 的縱坐標,再求
的縱坐標,再求![]() 、
、![]() 的長,即得到
的長,即得到![]() 為定值.
為定值.
解:(1)∵拋物線y=x2+bx+c經過點A(1,0),C(0,﹣3)
![]()
![]() 解得:
解得:![]()
∴拋物線的函數表達式為y=x2+2x﹣3
(2)①若點P在x軸下方,如圖1,
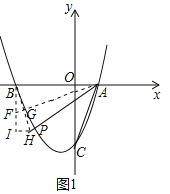
延長AP到H,使AH=AB,過點B作BI⊥x軸,連接BH,作BH中點G,連接并延長AG交BI于點F,過點H作HI⊥BI于點I
∵當x2+2x﹣3=0,解得:x1=﹣3,x2=1
∴B(﹣3,)
∵A(1,0),C(0,﹣3)
![]() ,
,![]() ,
,![]() ,
,![]()
![]() 中,
中,![]() ,
,![]()
∵AB=AH,G為BH中點
∴AG⊥BH,BG=GH
∴∠BAG=∠HAG,即∠PAB=2∠BAG
∵∠PAB=2∠ACO
∴∠BAG=∠ACO
![]() 中,
中,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,即
,即![]() ,
,![]()
設直線![]() 解析式為
解析式為![]()
![]()
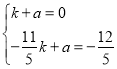 解得:
解得: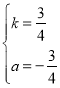
![]() 直線
直線![]()
![]()
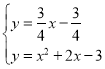 解得:
解得: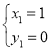 (即點
(即點![]() ,
,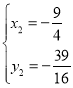
![]() ,
,![]() ;
;
②若點![]() 在
在![]() 軸上方,如圖2,
軸上方,如圖2,
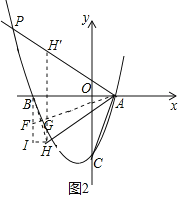
在![]() 上截取
上截取![]() ,則
,則![]() 與
與![]() 關于
關于![]() 軸對稱
軸對稱
![]() ,
,![]()
設直線![]() 解析式為
解析式為![]()
![]()
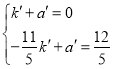 解得:
解得:
![]() 直線
直線![]()
![]()
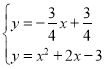 解得:
解得: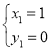 (即點
(即點![]() ,
,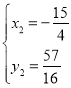
![]() ,
,![]() .
.
綜上所述,點![]() 的坐標為
的坐標為![]() ,
,![]() 或
或![]() ,
,![]() .
.
(3)![]() 為定值,
為定值,
![]() 拋物線
拋物線![]() 的對稱軸為:直線
的對稱軸為:直線![]()
![]() ,
,![]()
設![]() ,
,![]()
設直線![]() 解析式為
解析式為![]()
![]()
![]() 解得:
解得: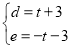
![]() 直線
直線![]()
當![]() 時,
時,![]()
![]()
設直線![]() 解析式為
解析式為![]()
![]()
![]() 解得:
解得:![]()
![]() 直線
直線![]()
當![]() 時,
時,![]()
![]()
![]() ,為定值.
,為定值.


科目:初中數學 來源: 題型:
【題目】如圖所示,在坡角為30°的山坡上有一豎立的旗桿AB,其正前方矗立一墻,當陽光與水平線成45°角時,測得旗桿AB落在坡上的影子BD的長為8米,落在墻上的影子CD的長為6米,求旗桿AB的高(結果保留根號).
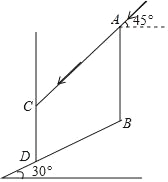
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某班甲、乙、丙三位同學最近5次數學成績及其所在班級相應平均分的折線統計圖,則下列判斷錯誤的是( ).

A. 甲的數學成績高于班級平均分,且成績比較穩定
B. 乙的數學成績在班級平均分附近波動,且比丙好
C. 丙的數學成績低于班級平均分,但成績逐次提高
D. 就甲、乙、丙三個人而言,乙的數學成績最不穩
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AD是△ABC的中線P是線段AD上的一點(不與點A、D重合),連接PB、PC,E、F、G、H分別是AB、AC、PB、PC的中點,AD與EF交于點M;
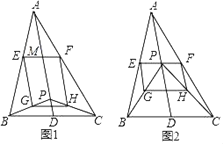
(1)如圖1,當AB=AC時,求證:四邊形EGHF是矩形;
(2)如圖2,當點P與點M重合時,在不添加任何輔助線的條件下,寫出所有與△BPE面積相等的三角形(不包括△BPE本身).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某環衛公司承包了市區兩個片區道路的清掃任務,需要購買某廠家A,B兩種型號的馬路清掃車,購買5輛A型馬路清掃車和6輛B型馬路清掃車共需171萬元;購買3輛A型馬路清掃車和12輛B型馬路清掃車共需237萬元.
(1)求這兩種馬路清掃車的單價;
(2)恰逢該廠舉行30周年慶,決定對這兩種馬路清掃車開展促銷活動,具體方案如下:購買A型馬路清掃車按原價的八折銷售,購買B型馬上清掃車不超過10輛時按原價銷售,超過10輛的部分按原價的七折銷售.設購買x輛A種馬路清掃車需要y1元,購買x(x>0)個B型馬路清掃車需要y2元,分別求出y1,y2關于x的函數關系式;
(3)若該公司承包的道路清掃面積為118000m2,每輛A型馬路清掃車每天清掃5000m2,每輛B型馬路清掃車每天清掃6000m2,公司準備購買20輛馬路清掃車,且B型馬路清掃車的數量大于10.請你幫該公司設計出最省錢的購買方案.請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小雪和小松分別從家和圖書館出發,沿同一條筆直的馬路相向而行.小雪開始跑步,中途在某地改為步行,且步行的速度為跑步速度的一半,小雪先出發5分鐘后,小松才騎自行車勻速回家.小雪到達圖書館恰好用了35分鐘.兩人之間的距離y(m)與小雪離開出發地的時間x(min)之間的函數圖象如圖所示,則當小松剛到家時,小雪離圖書館的距離為____米.
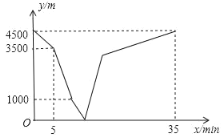
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線經過A(﹣2,0),B(0,2),C(![]() ,0)三點,一動點P從原點出發以1個單位/秒的速度沿x軸正方向運動,連接BP,過點A作直線BP的垂線交y軸于點Q.設點P的運動時間為t秒.
,0)三點,一動點P從原點出發以1個單位/秒的速度沿x軸正方向運動,連接BP,過點A作直線BP的垂線交y軸于點Q.設點P的運動時間為t秒.
(1)求拋物線的解析式;
(2)當BQ=![]() AP時,求t的值;
AP時,求t的值;
(3)隨著點P的運動,拋物線上是否存在一點M,使△MPQ為等邊三角形?若存在,請直接寫t的值及相應點M的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com