【題目】一元二次方程x2﹣2x=0的解是 ．
新思維假期作業寒假吉林大學出版社系列答案科目：初中數學 來源： 題型：
【題目】如圖，要設計一副寬20cm、長30cm的圖案，其中有兩橫兩豎的彩條，橫、豎彩條的寬度比為2：3，如果要使彩條所占面積是圖案面積的
，應如何設計彩條的寬度？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖①，直線MN⊥直線PQ，垂足為O，點A在射線OP上，點B在射線OQ上(A、B不與O點重合)，點C在射線ON上且OC=2，過點C作直線
∥PQ，點D在點C的左邊且CD=3.
(1) 直接寫出△BCD的面積.
(2) 如圖②，若AC⊥BC,作∠CBA的平分線交OC于E，交AC于F，則∠CEF與∠CFE有何數量關系？請說明理由.
(3) 如圖③，若∠ADC=∠DAC,點B在射線OQ上運動，∠ACB的平分線交DA的延長線于點H，在點B運動過程中
的值是否變化？若不變，直接寫出其值；若變化，直接寫出變化范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】
（1）請你根據圖中A、B兩點的位置，分別寫出它們所表示的有理數
A： _________ B： _________ ；
（2）觀察數軸，與點A的距離為4的點表示的數是：__________ ；
（3）若將數軸折疊，使得A點與－3表示的點重合，則B點與數____表示的點重合；
（4）若數軸上M、N兩點之間的距離為2016(M在N的左側)，且M、N兩點經過(3)中折疊后互相重合，則M、N兩點表示的數分別是：
M： N： .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小武新家裝修，在裝修客廳時，購進彩色地磚和單色地磚共100塊，共花費5600元．已知彩色地磚的單價是80元/塊，單色地磚的單價是40元/塊．
（1）兩種型號的地磚各采購了多少塊？
（2）如果廚房也要鋪設這兩種型號的地磚共60塊，且采購地磚的費用不超過3200元，那么彩色地磚最多能采購多少塊？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，∠C=90°，BC=7cm，AC=5，點P從B點出發，沿BC方向以2m/s的速度移動，點Q從C出發，沿CA方向以1m/s的速度移動．
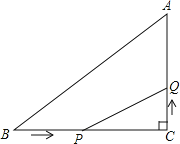
（1）若P、Q同時分別從B、C出發，那么幾秒后，△PCQ的面積等于4？
（2）若P、Q同時分別從B、C出發，那么幾秒后，PQ的長度等于5？
（3）△PCQ的面積何時最大，最大面積是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
