
【題目】如圖,在矩形ABCD中,AB=6,BC=8,點M,N同時從點B出發,分別在BC,BA上運動,若點M的運動速度是每秒2個單位長度,且是點N運動速度的2倍,當其中一個點到達終點時,停止一切運動.以MN為對稱軸作△MNB的對稱圖形△MNB1.點B1恰好在AD上的時間為______秒.在整個運動過程中,△MNB1與矩形ABCD重疊部分面積的最大值為______.

【答案】![]()
![]()
【解析】
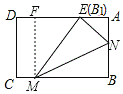
(1)如圖,當B′與AD交于點E,作FM⊥AD于F,根據軸對稱的性質可以得出ME=MB=2t,由勾股定理就可以表示出EF,就可以表示出AE,再由勾股定理就可以求出t的值;
(2)根據三角形的面積公式,分情況討論,當0<t≤![]() 和
和![]() <t≤4時由求分段函數的方法就可以求出結論.
<t≤4時由求分段函數的方法就可以求出結論.
(1)如下圖,當B′與AD交于點E,作FM⊥AD于F.
∴∠DFM=90°.
∵四邊形ABCD是矩形,
∴CD=AB.AD=BC.∠D=∠C=90°.
∴四邊形DCMF是矩形,
∴CD=MF.
∵△MNB與△MNE關于MN對稱,
∴△MNB≌△MNE,
∴ME=MB,NE=BN.
∵BN=t,BM=2t,
∴EN=t,ME=2t.
∵AB=6,BC=8,
∴CD=MF=6,CB=DA=8.AN=6-t
在Rt△MEF和Rt△AEN中,由勾股定理,得
EF=![]() ,AE=
,AE=![]() ,
,
∴![]() +
+![]() =2t,
=2t,
∴t=![]() .
.
(2)如圖所示:
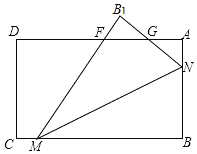
∵△MNB1與△MNB關于MN對稱,
∴∠MB1N=∠MBN=90°.
∵∠MB1N+∠MBN+∠B1MB+∠B1NB=360°,
∴∠B1MB+∠B1NB=180°.
∵∠B1NA+∠B1NB=180°,
∴∠B1NA=∠B1MB.
在變化過程中![]() ,∴∠B1NA不變
,∴∠B1NA不變
由(1)得tan∠B1NA=![]() ,
,
∴tan∠B1MB=![]() .
.
∵四邊形ABCD是矩形,
∴AD∥BC,
∴∠B1FG=∠B1MB.
∵BN=t,BM=2t,
∴B1N=t,MB1=2t.
∵AB=6,BC=8,
∴CD=MF=6,CB=DA=8.AN=6-t
∴GA=![]() (6-t),GN=
(6-t),GN=![]() (6-t),
(6-t),
∵B1G=B1N-GN=t-![]() (6-t)=
(6-t)=![]() t-10,
t-10,
∴B1F=(![]() t-10)×
t-10)×![]() =2t-
=2t-![]() .
.
∴當![]() <t≤4時,
<t≤4時,
S=t2-![]() (2t-
(2t-![]() )(
)(![]() t-10)=-
t-10)=-![]() (t-6)2+
(t-6)2+![]() ,
,
∴t=4時,S最大=![]() .
.
當0<t≤![]() 時,S=t2.
時,S=t2.
∴t=![]() 時,S最大=
時,S最大=![]() .
.
∵![]() >
>![]() .
.
∴最大值為![]() .
.
故答案為:(1)![]() ;(2)
;(2)![]() .
.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,是一輛小汽車與墻平行停放的平面示意圖,汽車靠墻一側OB與墻MN平行且距離為0.8米,一輛小汽車車門寬AO為1.2米,當車門打開角度∠AOB為40°時,車門是否會碰到墻?______;(填“是”或“否”)請簡述你的理由_______.(參考數據:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABD與△GDF都是等腰直角三角形,BD與DF均為斜邊(BD<DF).
(1)如圖1,B,D,F在同一直線上,過F作MF⊥GF于點F,取MF=AB,連結AM交BF于點H,連結GA,GM.
①求證:AH=HM;
②請判斷△GAM的形狀,并給予證明;
③請用等式表示線段AM,BD,DF的數量關系,并說明理由.
(2)如圖2,GD⊥BD,連結BF,取BF的中點H,連結AH并延長交DF于點M,請用等式直接寫出線段AM,BD,DF的數量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義一種對正整數n的“F”運算:①當n為奇數時,F(n)=3n+1;②當n為偶數時,F(n)=![]() (其中k是使F(n)為奇數的正整數)……,兩種運算交替重復進行,例如,取n=24,則:
(其中k是使F(n)為奇數的正整數)……,兩種運算交替重復進行,例如,取n=24,則:
![]()
若n=13,則第2018次“F”運算的結果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A(﹣1,0),B(3,0),C(0,1)在拋物線y=ax2+bx+c上.
(1)求拋物線解析式;
(2)在直線BC上方的拋物線上求一點P,使△PBC面積為1;
(3)在x軸下方且在拋物線對稱軸上,是否存在一點Q,使∠BQC=∠BAC?若存在,求出Q點坐標;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是邊長為3的等邊三角形,△BDC是等腰三角形,且∠BDC=120°.以點D為頂點作一個60°角,使其兩邊分別交AB于點M,交AC于點N,連接MN.
(1)求證:MN=BM+NC;
(2)求△AMN的周長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,E、F分別是AB、BC邊的中點,EP⊥CD于點P,∠BAD=110°,則∠FPC的度數是( )

A. 35° B. 45° C. 50° D. 55°
查看答案和解析>>
科目:初中數學 來源: 題型:
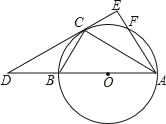
【題目】如圖,已知△ABC內接于⊙O,AB是⊙O的直徑,點F在⊙O上,且點C是![]() 的中點,過點C作⊙O的切線交AB的延長線于點D,交AF的延長線于點E.
的中點,過點C作⊙O的切線交AB的延長線于點D,交AF的延長線于點E.
(1)求證:AE⊥DE;
(2)若∠BAF=60°,AF=4,求CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“五一”期間,小明一家乘坐高鐵前往某市旅游,計劃第二天租用新能源汽車自駕出游。
 [來
[來
根據以上信息,解答下列問題:
(1)設租車時間為![]() 小時,租用甲公司的車所需費用為
小時,租用甲公司的車所需費用為![]() 元,租用乙公司的車所需費用為
元,租用乙公司的車所需費用為![]() 元,分別求出
元,分別求出![]() ,
,![]() 關于
關于![]() 的函數表達式;
的函數表達式;
(2)請你幫助小明計算并選擇哪個出游方案合算。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com