【題目】某市“藝術節”期間，小明、小亮都想去觀看茶藝表演，但是只有一張茶藝表演 門票，他們決定采用抽卡片的辦法確定誰去.規則如下：
將正面分別標有數字 1、2、3、4 的四張卡片（除數字外其余都相同）洗勻后，背面朝上 放置在桌面上，隨機抽出一張記下數字后放回；重新洗勻后背面朝上放置在桌面上， 再隨機抽出一張記下數字.如果兩個數字之和為奇數，則小明去；如果兩個數字之和 為偶數，則小亮去.
（1）請用列表或畫樹狀圖的方法表示抽出的兩張卡片上的數字之和的所有可能出現 的結果；
（2）你認為這個規則公平嗎？請說明理由.
科目：初中數學 來源： 題型：
【題目】蝸牛從某點O開始沿東西方向直線爬行，規定向東爬行的路程記為正數，向西爬行的路程記為負數．爬行的各段路程依次為（單位：厘米）：
.問：
（1）蝸牛最后是否回到出發點O？
（2）蝸牛離開出發點O最遠是多少厘米？
（3）在爬行過程中，如果每爬行1厘米獎勵一粒芝麻，則蝸牛可得到多少粒芝麻？
查看答案和解析>>
科目：初中數學 來源： 題型：
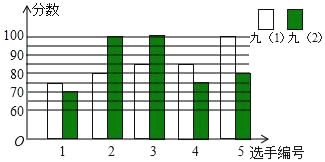
【題目】為選拔優秀選手參加瑤海區第八屆德育文化藝術節“誦經典”比賽活動，九年級（1）、（2）班根據初賽成績，各選出5名選手參加復賽，兩個班各選出的5名選手的復賽成績如圖所示
（1）根據圖示填寫下表
班級 | 平均數（分） | 中位數（分） | 眾數（分） |
九（1） | 85 |
| 85 |
九（2） |
| 80 |
|
（2）結合兩班復賽成績的平均數和中位數，分析哪個班級的復賽成績較好；
（3）計算兩班復賽成績的方差，并說明哪個班五名選手的成績較穩定．
查看答案和解析>>
科目：初中數學 來源： 題型：
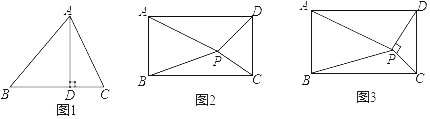
【題目】（幾何背景）如圖1，AD為銳角△ABC的高，垂足為D．求證：AB2﹣AC2＝BD2﹣CD2
（知識遷移）如圖2，矩形ABCD內任意一點P，連接PA、PB、PC、PD，請寫出PA、PB、PC、PD之間的數量關系，并說明理由．
（拓展應用）如圖3，矩形ABCD內一點P，PC⊥PD，若PA＝a，PB＝b，AB＝c，且a、b、c滿足a2﹣b2＝
c2，則
的值為 （請直接寫出結果）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，將拋物線
的對稱軸繞著點
（0，2）順時針旋轉45°后與該拋物線交于
兩點，點
是該拋物線上的一點．
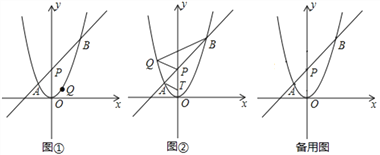
（1）求兩點的坐標。
（2）如圖①，若點在直線
的下方，求點到直線的距離的最大值；
（3）如圖②，若點在
軸左側，且點
是直線
上一點，當以
為頂點的三角形與
相似時，求所有滿足條件的
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，△ABC的坐標分別為A（﹣3，5），B（﹣4，2），C（﹣1，4）（注：每個方格的邊長均為1個單位長度）．
（1）將△ABC沿著水平方向向右平移6個單位得△A1B1C1，請畫出△A1B1C1；
（2）作出將△ABC關于O點成中心對稱的△A2B2C2，并直接寫出的坐標；
（3）△A1B1C1與△A2B2C2是否成中心對稱？若是，請寫出對稱中心的坐標；若不是，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖正方形ABCD中，點E、F分別在CD、BC邊上，△AEF是等邊三角形．以下結論：①EC＝FC；②∠AED＝75°；③AF＝
CE；④EF的垂直平分線是直線AC．正確結論個數有（ ）個．
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：初中數學 來源： 題型：
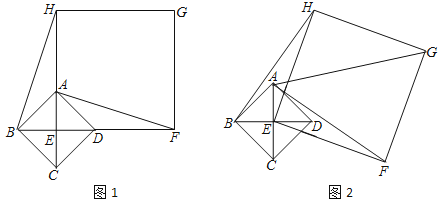
【題目】如圖1，已知四邊形ABCD是正方形，對角線AC、BD相交于點E，以點E為頂點作正方形EFGH．
（1）如圖1，點A、D分別在EH和EF上，連接BH、AF，BH和AF有何數量關系，并說明理由；
（2）將正方形EFGH繞點E順時針方向旋轉，如圖2，判斷BH和AF的數量關系，并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
