
【題目】如圖,已知△ABC中,AB=AC,BD⊥AC于點(diǎn)D,CE⊥AB于點(diǎn)E,CE和BD交于點(diǎn)O,AO的延長(zhǎng)線交BC于點(diǎn)F,則圖中全等的三角形有( )

A.8對(duì)B.7對(duì)C.6對(duì)D.5對(duì)

| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,正方形![]() 的邊長(zhǎng)為
的邊長(zhǎng)為![]() ,
,![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),![]() 、
、![]() 在坐標(biāo)軸上,把正方形
在坐標(biāo)軸上,把正方形![]() 繞點(diǎn)
繞點(diǎn)![]() 順時(shí)針旋轉(zhuǎn)后得到正方形
順時(shí)針旋轉(zhuǎn)后得到正方形![]() ,
,![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,且點(diǎn)
,且點(diǎn)![]() 恰為
恰為![]() 的中點(diǎn),則點(diǎn)
的中點(diǎn),則點(diǎn)![]() 的坐標(biāo)為________.
的坐標(biāo)為________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我校圖書館大樓工程在招標(biāo)時(shí),接到甲乙兩個(gè)工程隊(duì)的投標(biāo)書,每施工一個(gè)月,需付甲工程隊(duì)工程款16萬(wàn)元,付乙工程隊(duì)12萬(wàn)元。工程領(lǐng)導(dǎo)小組根據(jù)甲乙兩隊(duì)的投標(biāo)書測(cè)算,可有三種施工方案:
(1)甲隊(duì)單獨(dú)完成此項(xiàng)工程剛好如期完工;
(2)乙隊(duì)單獨(dú)完成此項(xiàng)工程要比規(guī)定工期多用3個(gè)月;
(3)若甲乙兩隊(duì)合作2個(gè)月,剩下的工程由乙隊(duì)獨(dú)做也正好如期完工。
你覺得哪一種施工方案最節(jié)省工程款,說明理由。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() ,則下列關(guān)于該函數(shù)的描述中,錯(cuò)誤的是( )
,則下列關(guān)于該函數(shù)的描述中,錯(cuò)誤的是( )
A. 該函數(shù)的最小值是![]()
B. 該函數(shù)圖象與![]() 軸沒有交點(diǎn)
軸沒有交點(diǎn)
C. 該函數(shù)圖象與![]() 軸有兩個(gè)不同的交點(diǎn)
軸有兩個(gè)不同的交點(diǎn)
D. 當(dāng)![]() 時(shí),
時(shí),![]() 隨著
隨著![]() 的增大而增大
的增大而增大
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
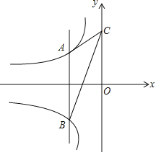
【題目】如圖,動(dòng)點(diǎn)![]() 在雙曲線
在雙曲線![]() 上,動(dòng)點(diǎn)
上,動(dòng)點(diǎn)![]() 在雙曲線
在雙曲線![]() 上,且直線
上,且直線![]() 軸,若點(diǎn)
軸,若點(diǎn)![]() 的坐標(biāo)是
的坐標(biāo)是![]() ,點(diǎn)
,點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() .
.
![]() 當(dāng)
當(dāng)![]() 取不同的值時(shí),
取不同的值時(shí),![]() 的面積________(填“變化”或者“不變化”);
的面積________(填“變化”或者“不變化”);
![]() 線段
線段![]() 的長(zhǎng)可以用
的長(zhǎng)可以用![]() 表示為________;
表示為________;
![]() 若點(diǎn)
若點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,請(qǐng)問是否存在常數(shù)
,請(qǐng)問是否存在常數(shù)![]() ,使得
,使得![]() 的面積等于
的面積等于![]() ?若有,請(qǐng)求出
?若有,請(qǐng)求出![]() 的值;若沒有,請(qǐng)說明理由.
的值;若沒有,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),將線段BC繞點(diǎn)B逆時(shí)針旋轉(zhuǎn)60°得到線段BD.
(1)如圖1,直接寫出∠ABD的大小(用含α的式子表示);
(2)如圖2,若∠BCE=150°,∠ABE=60°, ∠DEC=45°,求α的值;
(3)如圖3,若∠BCE=150°,∠ABE=60°,判斷△ABE的形狀并加以證明.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在某場(chǎng)足球比賽中,球員甲從球門底部中心點(diǎn)![]() 的正前方
的正前方![]() 處起腳射門,足球沿拋物線飛向球門中心線;當(dāng)足球飛離地面高度為
處起腳射門,足球沿拋物線飛向球門中心線;當(dāng)足球飛離地面高度為![]() 時(shí)達(dá)到最高點(diǎn),此時(shí)足球飛行的水平距離為
時(shí)達(dá)到最高點(diǎn),此時(shí)足球飛行的水平距離為![]() .已知球門的橫梁高
.已知球門的橫梁高![]() 為
為![]() .
.

![]() 在如圖所示的平面直角坐標(biāo)系中,問此飛行足球能否進(jìn)球門?(不計(jì)其它情況)
在如圖所示的平面直角坐標(biāo)系中,問此飛行足球能否進(jìn)球門?(不計(jì)其它情況)
![]() 守門員乙站在距離球門
守門員乙站在距離球門![]() 處,他跳起時(shí)手的最大摸高為
處,他跳起時(shí)手的最大摸高為![]() ,他能阻止球員甲的此次射門嗎?如果不能,他至少后退多遠(yuǎn)才能阻止球員甲的射門?
,他能阻止球員甲的此次射門嗎?如果不能,他至少后退多遠(yuǎn)才能阻止球員甲的射門?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,二次函數(shù)
中,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸正半軸交于
軸正半軸交于![]() 點(diǎn).
點(diǎn).

![]() 求證:該二次函數(shù)的圖象與
求證:該二次函數(shù)的圖象與![]() 軸必有兩個(gè)交點(diǎn);
軸必有兩個(gè)交點(diǎn);
![]() 設(shè)該二次函數(shù)的圖象與
設(shè)該二次函數(shù)的圖象與![]() 軸的兩個(gè)交點(diǎn)中右側(cè)的交點(diǎn)為點(diǎn)
軸的兩個(gè)交點(diǎn)中右側(cè)的交點(diǎn)為點(diǎn)![]() ,若
,若![]() ,將直線
,將直線![]() 向下平移
向下平移![]() 個(gè)單位得到直線
個(gè)單位得到直線![]() ,求直線
,求直線![]() 的解析式;
的解析式;
![]() 在
在![]() 的條件下,設(shè)
的條件下,設(shè)![]() 為二次函數(shù)圖象上的一個(gè)動(dòng)點(diǎn),當(dāng)
為二次函數(shù)圖象上的一個(gè)動(dòng)點(diǎn),當(dāng)![]() 時(shí),點(diǎn)
時(shí),點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸的對(duì)稱點(diǎn)都在直線
軸的對(duì)稱點(diǎn)都在直線![]() 的下方,求
的下方,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com