【題目】為創建“美麗鄉村”，某村計劃購買甲、乙兩種樹苗共400棵，對本村道路進行綠化改造，已知甲種樹苗每棵200元，乙種樹苗每棵300元．
若購買兩種樹苗的總金額為90000元，求需購買甲、乙兩種樹苗各多少棵？
若購買甲種樹苗的金額不少于購買乙種樹苗的金額，則至少應購買甲種樹苗多少棵？
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖，直線OC、BC的函數關系式分別是y1＝x和y2＝﹣2x+6，直線BC與x軸交于點B，直線BA與直線OC相交于點A．
（1）當x取何值時y1＞y2？
（2）當直線BA平分△BOC的面積時，求點A的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，在平面直角坐標系中，點A在x軸上，直線OC上所有的點坐標
，都是二元一次方程
的解，直線AC上所有的點坐標，都是二元一次方程
的解，過C作x軸的平行線，交y軸與點B．
（1）求點A、B、C的坐標；
（2）如圖②，點M、N分別為線段BC，OA上的兩個動點，點M從點C以每秒1個單位長度的速度向左運動，同時點N從點O以每秒1．5個單位長度的速度向右運動，設運動時間為t秒，且0＜t＜4，試比較四邊形MNAC的面積與四邊形MNOB的面積的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ABC和∠ACB的平分線相交于點O，過點O作EF∥BC交AB于E，交AC于F，過點O作OD⊥AC于D，下列四個結論：
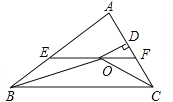
①EF=BE+CF；
②∠BOC=90°+
∠A；
③點O到△ABC各邊的距離相等；
④設OD=m，AE+AF=n，則
．
其中正確的結論是____．（填序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知某項工程由甲、乙兩隊合做12天可以完成，共需工程費用27720元．乙隊單獨完成這項工程所需時間是甲隊單獨完成這項工程所需時間的1.5倍，且甲隊每天的工程費用比乙隊多250元．
（1）求甲、乙兩隊單獨完成這項工程各需多少天？
（2）若工程管理部門決定從這兩個隊中選一個隊單獨完成此項工程，從節約資金的角度考慮，應選擇哪個工程隊？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
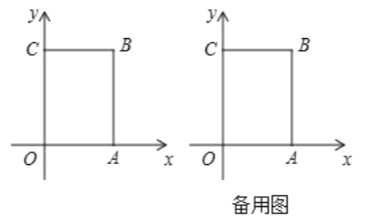
【題目】如圖，在長方形
中，
為平面直角坐標系的原點，點
的坐標為
，點
的坐標為
且
滿足
，點
在第一象限內，點
從原點出發，以每秒
個單位長度的速度沿著
的線路移動．
求點的坐標為 ；當點移動
秒時，點的坐標為
在移動過程中，當點移動
秒時，求
的面積．
在的條件下，坐標軸上是否存在點
，使
的面積與的面積相等，若存在，求點的坐標；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把拋物線y= 
x2平移得到拋物線m，拋物線m經過點A（﹣6，0）和原點O（0，0），它的頂點為P，它的對稱軸與拋物線y= x2交于點Q，則圖中陰影部分的面積為 ． 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖1，a∥b，則∠1+∠2=
（2）如圖2，AB∥CD，則∠1+∠2+∠3= ，并說明理由
（3）如圖3，a∥b，則∠1+∠2+∠3+∠4=
（4）如圖4，a∥b，根據以上結論，試探究∠1+∠2+∠3+∠4+…+∠n= （直接寫出你的結論，無需說明理由）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】旋轉變換是解決數學問題中一種重要的思想方法，通過旋轉變換可以將分散的條件集中到一起，從而方便解決問題.已知，
中，
，
，點
、
在邊
上，且
.
（1）如圖
，當
時，將
繞點
順時針旋轉
到
的位置，連接
，
①求
的度數；
②求證：
；
（2）如圖
，當
時，猜想
、
、
的數量關系，并說明理由；
（3）如圖
，當
，
，
時，請直接寫出的長為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
