
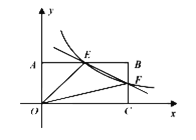
【題目】如圖,在直角坐標系中,點B的坐標為![]() ,過點B分別作x軸、y軸垂線,垂足分別是C,A,反比例函數(shù)
,過點B分別作x軸、y軸垂線,垂足分別是C,A,反比例函數(shù)![]() 的圖象交AB,BC分別于點E,F.
的圖象交AB,BC分別于點E,F.

(1)求直線EF的解析式.
(2)求四邊形BEOF的面積.
(3)若點P在y軸上,且![]() 是等腰三角形,請直接寫出點P的坐標.
是等腰三角形,請直接寫出點P的坐標.
【答案】(1)![]() ;(2)1;(3)點P的坐標為
;(2)1;(3)點P的坐標為![]() 或
或![]() .
.
【解析】
(1)點E與點B的縱坐標相同,點F與點B的橫坐標相同,分別將y=1,x=2代入反比例函數(shù)解析式,可求出E、F的坐標,然后采用待定系數(shù)法即可求出直線EF的解析式;
(2)利用![]() 即可求出答案;
即可求出答案;
(3)設P點坐標為(0,m),分別討論OP=OE,OP=PE,OE=PE三種情況,利用兩點間的距離公式求出m即可得到P點坐標.
解:(1)![]() 軸,
軸,![]() 軸,
軸,
將![]() 代入
代入![]() ,得
,得![]()
![]()
將![]() 代入
代入![]() 得:
得:![]() ,
,
![]()
設直線EF的解析式為![]()
把E、F的坐標代入![]() 解得
解得
![]()
∴直線EF的解析式為![]()
(2)由題意可得:
![]()
![]()
=1
(3)設P點坐標為(0,m),
∵E(1,1),
∴![]() ,
,![]() ,
,![]()
①當OP=OE時,![]() ,解得
,解得![]() ,
,![]()
∴P點坐標為![]() 或
或![]()
②當OP=PE時,![]() ,解得
,解得![]()
∴P點坐標為![]()
③當OE=PE時,![]() ,解得
,解得![]() ,
,![]()
當m=0時,P與原點重合,不符合題意,舍去,
∴P點坐標為![]()
綜上所述,點P的坐標為![]() 或
或![]()


 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:初中數(shù)學 來源: 題型:
【題目】作圖題:(保留作圖痕跡,不寫做法)
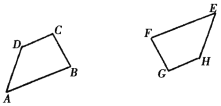
(1)已知:如圖,四邊形ABCD與四邊形EFGH成中心對稱,試畫出它們的對稱中心O。
(2)考古學家在考古過程中發(fā)現(xiàn)一個圓盤,但是因為歷史悠久,已經(jīng)有一部分缺失,如圖所示.現(xiàn)希望復原圓盤,需要先找到圓盤的圓心,才能繼續(xù)完成后續(xù)修復工作.請利用直尺(無刻度)和圓規(guī),在圖中找出圓心O.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在一個不透明的盒子中裝有大小和形狀相同的3個紅球和2個白球,把它們充分攪勻.
(1)“從中任意抽取1個球不是紅球就是白球”是 事件,“從中任意抽取1個球是黑球”是 事件;
(2)從中任意抽取1個球恰好是紅球的概率是 ;
(3)學校決定在甲、乙兩名同學中選取一名作為學生代表發(fā)言,制定如下規(guī)則:從盒子中任取兩個球,若兩球同色,則選甲;若兩球異色,則選乙.甲、乙兩名同學被選中的概率各是多少?你認為這個規(guī)則公平嗎?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
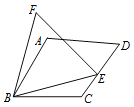
【題目】如圖7,在四邊形ABCD中,AB=BC,∠ABC=60°,E是CD邊上一點,連接BE,以BE為一邊作等邊三角形BEF.請用直尺在圖中連接一條線段,使圖中存在經(jīng)過旋轉可完全重合的兩個三角形,并說明這兩個三角形經(jīng)過什么樣的旋轉可重合.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
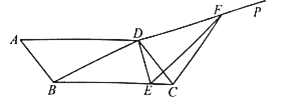
【題目】如圖,在![]() 中,
中,![]() ,對角線
,對角線![]() ,點E是線段BC上的動點,連接DE,過點D作DP⊥DE,在射線DP上取點F,使得
,點E是線段BC上的動點,連接DE,過點D作DP⊥DE,在射線DP上取點F,使得![]() ,連接CF,則
,連接CF,則![]() 周長的最小值為___________.
周長的最小值為___________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,在矩形ABCD中,點P是BC邊上一點,連接AP交對角線BD于點E,![]() .作線段AP的中垂線MN分別交線段DC,DB,AP,AB于點M,G,F,N.
.作線段AP的中垂線MN分別交線段DC,DB,AP,AB于點M,G,F,N.
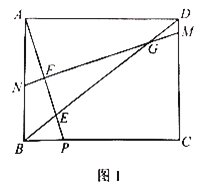
(1)求證:![]() ;
;
(2)若![]() ,求
,求![]() .
.
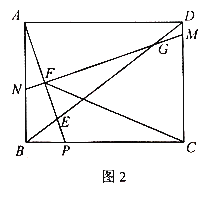
(3)如圖2,在(2)的條件下,連接CF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某公司銷售一種新型產(chǎn)品,現(xiàn)準備從國內(nèi)和國外兩種銷售方案中選擇一種進行銷售.若只在國內(nèi)銷售,銷售價格y(元/件)與月銷量x(件)的函數(shù)關系式為y=-![]() x+150,成本為50元/件,無論銷售多少,每月還需支出廣告費90000元,設月利潤為w內(nèi)(元),若只在國外銷售,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數(shù),10
x+150,成本為50元/件,無論銷售多少,每月還需支出廣告費90000元,設月利潤為w內(nèi)(元),若只在國外銷售,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數(shù),10![]() a
a![]() 40),當月銷量為x(件)時,每月還需繳納
40),當月銷量為x(件)時,每月還需繳納![]() x2元的附加費,設月利潤為w外(元).
x2元的附加費,設月利潤為w外(元).
(1)當x=1000時,y= 元/件,w內(nèi)= 元;
(2)分別求出w內(nèi),w外與x間的函數(shù)關系式(不必寫x的取值范圍);
(3)當x為何值時,在國內(nèi)銷售的月利潤最大?若在國外銷售月利潤的最大值與在國內(nèi)銷售月利潤的最大值相同,求a的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,點D在AB上,以AD為直徑的⊙O與邊BC相切于點E,與邊AC相交于點G,且![]() =
=![]() ,連接GO并延長交⊙O于點F,連接BF
,連接GO并延長交⊙O于點F,連接BF
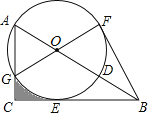
(1)求證:①AO=AG,②BF是⊙O的切線.
(2)若BD=6,求圖形中陰影部分的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】圖①是由一個完全相同的小正方體組成的立體圖形,將圖①中的一個小正方體改變位置后如圖②,則三視圖發(fā)生改變的是( )
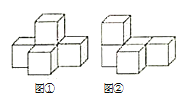
A. 主視圖,俯視較和左視圖都改變
B. 左視圖
C. 俯視圖
D. 主視圖
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com