
【題目】已知一次函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像交于點
的圖像交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,若
,若![]() ,且
,且![]() .
.

(1)求反比例函數與一次函數的表達式;
(2)若點![]() 為
為![]() 軸上一點,
軸上一點,![]() 是等腰三角形,求點
是等腰三角形,求點![]() 的坐標.
的坐標.
【答案】(1)反比例函數的表達式為![]() ,直線
,直線![]() 的表達式為
的表達式為![]() ;(2)
;(2)![]() 的坐標為
的坐標為![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1) 過點![]() 作
作![]() 軸于
軸于![]() ,根據和
,根據和![]() 求出AD的長度,再利用
求出AD的長度,再利用![]() 和勾股定理得到BD的長度,進而得到答案;
和勾股定理得到BD的長度,進而得到答案;
(2)根據得到的![]() 是等腰三角形分情況
是等腰三角形分情況![]() 、
、![]() 、
、![]() 討論即可得到答案;
討論即可得到答案;
解:(1)如圖,過點![]() 作
作![]() 軸于
軸于![]() ,
,

∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() (勾股定理),
(勾股定理),
∴![]() ,
,
∴![]() ,
,
將點![]() 坐標代入反比例函數
坐標代入反比例函數![]() 中得,
中得,![]() ,
,
∴反比例函數的表達式為![]() ,
,
將點![]() ,
,![]() 代入
代入![]() 中,
中,
得:![]() ,
,
解得: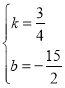
∴直線![]() 的表達式為
的表達式為![]()
(2)由(1)知,![]() ,
,
∵![]() 是等腰三角形,
是等腰三角形,
∴①當![]() 時,
時,
∴![]() ,
,
∴![]() 或
或![]() ,
,
②當![]() 時,如圖:
時,如圖:
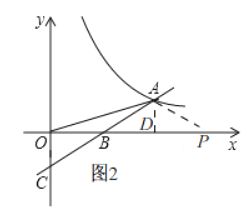
由(1)知,![]() ,
,
易知,點![]() 與點
與點![]() 關于
關于![]() 對稱,
對稱,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
③當![]() 時,設
時,設![]() ,
,
∵![]() ,
,![]() ,
,
∴根據兩點間的距離公式得到:![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
即:滿足條件的點![]() 的坐標為
的坐標為![]() 或
或![]() 或
或![]() 或
或![]() .
.


 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數系列答案
同步奧數系列答案科目:初中數學 來源: 題型:
【題目】已知y關于x的二次函數y=x-bx+![]() b+b-5的圖象與x軸有兩個公共點.
b+b-5的圖象與x軸有兩個公共點.
(1)求b的取值范圍;
(2)若b取滿足條件的最大整數值,當m≤x≤![]() 時,函數y的取值范圍是n≤y≤6-2m,求m,n的值;
時,函數y的取值范圍是n≤y≤6-2m,求m,n的值;
(3)若在自變量x的值滿足b≤x≤b+3的情況下,對應函數y的最小值為![]() ,求此時二次函數的解析式.
,求此時二次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BM是以AB為直徑的⊙O的切線,B為切點,BC平分∠ABM,弦CD交AB于點E,DE=OE.

(1)求證:△ACB是等腰直角三角形;
(2)求證:OA2=OEDC:
(3)求tan∠ACD的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】只有1和它本身兩個因數且大于1的正整數叫做素數.我國數學家陳景潤哥德巴赫猜想的研究中取得了世界領先的成果.哥德巴赫猜想是“每個大于2的偶數都表示為兩個素數的和”,如10=3+7.
(1)從7,11,13,17這4個素數中隨機抽取一個,則抽到的數是11的概率是_____;
(2)從7,11,13,17這4個素數中隨機抽取1個數,再從余下的3個數中隨機抽取1個數,用畫樹狀圖或列表的方法,求抽到的兩個素數之和等于24的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,∠C=30°,過D作DE⊥BC于點E,延長CB至點F,使BF=CE,連接AF.若AF=4,CF=10![]() ,則ABCD的面積為_____.
,則ABCD的面積為_____.
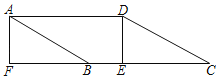
查看答案和解析>>
科目:初中數學 來源: 題型:
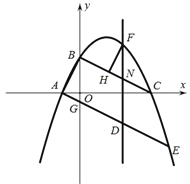
【題目】如圖所示,在平面直角坐標系中,拋物線![]() 與y軸交于點B,與x軸交于點A,C(點A在點C的左側),A(-1,0),C(4,0),連接AB,BC,點
與y軸交于點B,與x軸交于點A,C(點A在點C的左側),A(-1,0),C(4,0),連接AB,BC,點![]() 為y軸負半軸上的一點,連接AG并延長交拋物線于點E,點D為線段AE上的一個動點,過點D作y軸的平行線交拋物線于點F,與線段BC交于點N.
為y軸負半軸上的一點,連接AG并延長交拋物線于點E,點D為線段AE上的一個動點,過點D作y軸的平行線交拋物線于點F,與線段BC交于點N.
(1)求拋物線的表達式及直線BC的表達式;
(2)在點D運動的過程中,當FN的值最大時,在線段BC上是否存在一點H,使得FNH與ABC相似,如果存在,求出此時H點的坐標;
(3)當DF=4時,連接DC,四邊形ABCD先向上平移一定單位長度后,使點D落在x軸上,然后沿x軸向左平移n(1n4)個單位長度,用含n的表達式表示平移后的四邊形與原四邊形重疊部分的面積S(直接寫出結果).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com