
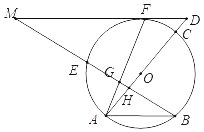
【題目】如圖,F為⊙O上的一點,過點F作⊙O的切線與直徑AC的延長線交于點D,過圓上的另一點B作AO的垂線,交DF的延長線于點M,交⊙O于點E,垂足為H,連接AF,交BM于點G.
(1)求證:△MFG為等腰三角形.
(2)若AB∥MD,求MF、FG、EG之間的數量關系,并說明理由.
(3)在(2)的條件下,若DF=6,tan∠M=![]() ,求AG的長.
,求AG的長.
【答案】(1)詳見解析;(2)FG2=EGMF,理由詳見解析;(3)![]() .
.
【解析】
(1)連接OF,由切線的性質結合等角的余角相等可得出∠MFG=∠AGH,進而得出∠MFG=∠MGF,可證出△MFG為等腰三角形;
(2)由MD∥AB可得出∠M=∠B,連接EF,則∠EFG=∠B,進而可得出∠M=∠EFG,結合∠MGF=∠FGE可得出△MGF∽△FGE,利用相似三角形的性質可得出FG2=EGMG,結合MF=MG可得出FG2=EGMF;
(3)由∠M=∠B,tan∠M=![]() ,設AH=3k,則HB=4k,AB=5k,連接FO,OB,由∠MHD=∠OFD=90°,∠D=∠D可得出∠FOD=∠M,結合FD=6,可得出FO=8=OB=OA,進而可得出OH=8﹣3k,在Rt△OHB中,利用勾股定理可求出k值,由MD∥AB可得出∠MFG=∠BAF,進而可得出∠BGA=∠BAG,由等角對等腰可得出AB=GB=5k,結合BH=4k可得出GH=k,結合AH=3k利用勾股定理可求出AG=
,設AH=3k,則HB=4k,AB=5k,連接FO,OB,由∠MHD=∠OFD=90°,∠D=∠D可得出∠FOD=∠M,結合FD=6,可得出FO=8=OB=OA,進而可得出OH=8﹣3k,在Rt△OHB中,利用勾股定理可求出k值,由MD∥AB可得出∠MFG=∠BAF,進而可得出∠BGA=∠BAG,由等角對等腰可得出AB=GB=5k,結合BH=4k可得出GH=k,結合AH=3k利用勾股定理可求出AG=![]() k,再代入k值即可求出結論.
k,再代入k值即可求出結論.
(1)證明:連接OF,如圖1所示.
∵DF為⊙O的切線,
∴OF⊥DM,
∴∠MFG+∠AFO=90°.
∵BH⊥AD,
∴∠AHG=90°,
∴∠AGH+∠GAH=90°.
∵OA=OF,
∴∠OAF=∠OFA,
∴∠MFG=∠AGH.
又∵∠MGF=∠AGH,
∴∠MFG=∠MGF,
∴△MFG為等腰三角形.
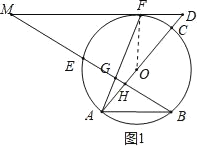
(2)解:FG2=EGMF,理由如下:
∵MD∥AB,
∴∠M=∠B.
連接EF,如圖2所示.
∵∠EFG=∠B,
∴∠M=∠EFG.
又∵∠MGF=∠FGE,
∴△MGF∽△FGE,
∴![]() ,即FG2=EGMG,
,即FG2=EGMG,
∴FG2=EGMF.
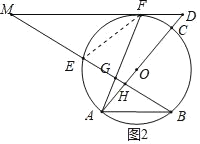
(3)解:∵∠M=∠B,tan∠M=![]() ,
,
∴設AH=3k,則HB=4k,AB=5k.
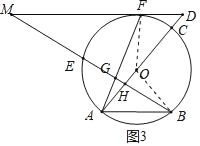
連接FO,OB,如圖3所示.
∵∠MHD=∠OFD=90°,∠D=∠D,
∴∠FOD=∠
∵FD=6,
∴FO=8=OB=OA,
∴OH=8﹣3k.
在Rt△OHB中,OH2+HB2=OB2,即(4k)2+(8﹣3k)2=82,
解得:k=![]() .
.
∵MD∥AB,
∴∠MFG=∠BAF,
∴∠BGA=∠BAG,
∴AB=GB=5k,
∴GH=k,
∴AG=![]() k,(勾股定理)
k,(勾股定理)
∴AG=![]() .
.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
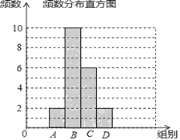
【題目】張老師把微信運動里“好友計步榜”排名前20的好友一天行走的步數做了整理,繪制了如下不完整的統計圖表:
組別 | 步數分組 | 頻率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合計 | 1 |
根據信息解答下列問題:
(1)填空:m= ,n= ;并補全條形統計圖;
(2)這20名朋友一天行走步數的中位數落在 組;(填組別)
(3)張老師準備隨機給排名前4名的甲、乙、丙、丁中的兩位點贊,請求出甲、乙被同時點贊的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
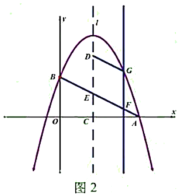
【題目】如圖,一次函數y=![]() x﹣2的圖象與x軸交于點A,與y軸交于點B,點D的坐標為(﹣1,0),二次函數y=ax2+bx+c(a≠0)的圖象經過A,B,D三點.
x﹣2的圖象與x軸交于點A,與y軸交于點B,點D的坐標為(﹣1,0),二次函數y=ax2+bx+c(a≠0)的圖象經過A,B,D三點.
(1)求二次函數的解析式;
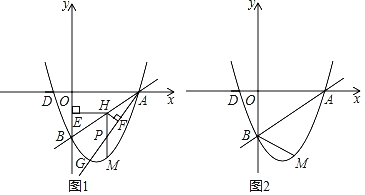
(2)如圖1,已知點G(1,m)在拋物線上,作射線AG,點H為線段AB上一點,過點H作HE⊥y軸于點E,過點H作HF⊥AG于點F,過點H作HM∥y軸交AG于點P,交拋物線于點M,當HEHF的值最大時,求HM的長;
(3)在(2)的條件下,連接BM,若點N為拋物線上一點,且滿足∠BMN=∠BAO,求點N的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣![]() x2+mx+n與x軸交于A、B兩點,與y軸交于點C,拋物線的對稱軸交x軸于點D,已知A(﹣1,0),C(0,2).
x2+mx+n與x軸交于A、B兩點,與y軸交于點C,拋物線的對稱軸交x軸于點D,已知A(﹣1,0),C(0,2).
(1)求拋物線的表達式;
(2)在拋物線的對稱軸上是否存在點P,使△PCD是以CD為腰的等腰三角形?如果存在,直接寫出P點的坐標;如果不存在,請說明理由;
(3)點E時線段BC上的一個動點,過點E作x軸的垂線與拋物線相交于點F,當點E運動到什么位置時,四邊形CDBF的面積最大?求出四邊形CDBF的最大面積及此時E點的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
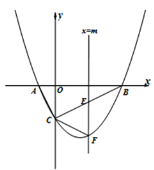
【題目】如圖,拋物線![]() 與x軸交于A、B兩點,與y軸交于點C,已知A(–1,0),且直線BC的解析式為y=
與x軸交于A、B兩點,與y軸交于點C,已知A(–1,0),且直線BC的解析式為y=![]() x-2,作垂直于x軸的直線
x-2,作垂直于x軸的直線![]() ,與拋物線交于點F,與線段BC交于點E(不與點B和點C重合).
,與拋物線交于點F,與線段BC交于點E(不與點B和點C重合).
(1)求拋物線的解析式;
(2)若△CEF是以CE為腰的等腰三角形,求m的值;
(3)點P為y軸左側拋物線上的一點,過點P作![]() 交直線BC于點M,連接PB,若以P、M、B為頂點的三角形與△ABC相似,求P點的坐標.
交直線BC于點M,連接PB,若以P、M、B為頂點的三角形與△ABC相似,求P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,E是對角線BD上的一點,過點C作CF∥DB,且CF=DE,連接AE,BF,EF.
(1)求證:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,則四邊形ABFE是什么特殊四邊形?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】家庭過期藥品屬于“國家危險廢物”,處理不當將污染環境,危害健康.某市藥監部門為了解市民家庭處理過期藥品的方式,決定對全市家庭作一次簡單隨機抽樣調査.
(1)下列選取樣本的方法最合理的一種是 .(只需填上正確答案的序號)
①在市中心某個居民區以家庭為單位隨機抽取;②在全市醫務工作者中以家庭為單位隨機抽取;③在全市常住人口中以家庭為單位隨機抽取.
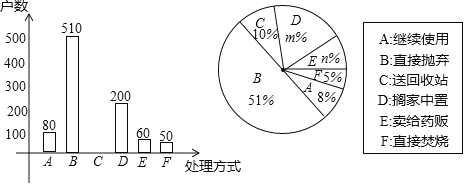
(2)本次抽樣調査發現,接受調査的家庭都有過期藥品,現將有關數據呈現如圖:
①m= ,n= ;
②補全條形統計圖;
③扇形統計圖中扇形C的圓心角度數是 ;
④家庭過期藥品的正確處理方式是送回收點,若該市有180萬戶家庭,請估計大約有多少戶家庭處理過期藥品的方式是送回收點.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年4月23日是第二十四個“世界讀書日“.某校組織讀書征文比賽活動,評選出一、二、三等獎若干名,并繪成如圖所示的條形統計圖和扇形統計圖(不完整),請你根據圖中信息解答下列問題:

(1)求本次比賽獲獎的總人數,并補全條形統計圖;
(2)求扇形統計圖中“二等獎”所對應扇形的圓心角度數;
(3)學校從甲、乙、丙、丁4位一等獎獲得者中隨機抽取2人參加“世界讀書日”宣傳活動,請用列表法或畫樹狀圖的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,拋物線![]() 與
與![]() 軸的一個交點為點
軸的一個交點為點![]() ,與
,與![]() 軸的交點為點
軸的交點為點![]() ,拋物線的對稱軸
,拋物線的對稱軸![]() 與
與![]() 軸交于點
軸交于點![]() ,與線段
,與線段![]() 交于點
交于點![]() ,點
,點![]() 是對稱軸
是對稱軸![]() 上一動點.
上一動點.

(1)點![]() 的坐標是________,點
的坐標是________,點![]() 的坐標是________;
的坐標是________;
(2)是否存在點![]() ,使得
,使得![]() 和
和![]() 相似?若存在,請求出點
相似?若存在,請求出點![]() 的坐標,若不存在,請說明理由;
的坐標,若不存在,請說明理由;
(3)如圖2,拋物線的對稱軸![]() 向右平移與線段
向右平移與線段![]() 交于點
交于點![]() ,與拋物線交于點
,與拋物線交于點![]() ,當四邊形
,當四邊形![]() 是平行四邊形且周長最大時,求出點
是平行四邊形且周長最大時,求出點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com