Question

【題目】如圖，在△ABC中，D為BC的中點，DE⊥BC交∠BAC的平分線AE于E，EF⊥AB于F，EG⊥AC交AC延長線于G．求證：BF=CG．

Answer 1

【答案】解：如圖，連接BE、EC，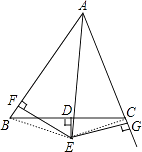

∵ED⊥BC，
D為BC中點，
∴BE=EC，
∵EF⊥AB EG⊥AG，
且AE平分∠FAG，
∴FE=EG，
在Rt△BFE和Rt△CGE中，
，
∴Rt△BFE≌Rt△CGE（HL），
∴BF=CG．
【解析】連接EB、EC，利用已知條件證明Rt△BEF≌Rt△CEG，即可得到BF=CG．
【考點精析】根據題目的已知條件，利用角平分線的性質定理和線段垂直平分線的性質的相關知識可以得到問題的答案，需要掌握定理1：在角的平分線上的點到這個角的兩邊的距離相等； 定理2：一個角的兩邊的距離相等的點，在這個角的平分線上；垂直于一條線段并且平分這條線段的直線是這條線段的垂直平分線；線段垂直平分線的性質定理：線段垂直平分線上的點和這條線段兩個端點的距離相等．