
(本題滿分12分)在平面直角坐標系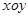 中,已知二次函數
中,已知二次函數 的圖象與x軸交于A,B兩點(點A在點B的左邊),AB=4,與y軸交于點C,且過點(2,3).
的圖象與x軸交于A,B兩點(點A在點B的左邊),AB=4,與y軸交于點C,且過點(2,3).
(1)求此二次函數的表達式;
(2)若拋物線的頂點為D,連接CD、CB,問拋物線上是否存在點P,使得∠PBC+∠BDC=90°. 若存在,求出點P的坐標;若不存在,請說明理由; (3)點K拋物線上C關于對稱軸的對稱點,點G拋物線上的動點,在x軸上是否存在點F,使A、K、F、G這樣的四個點為頂點的四邊形是平行四邊形?如果存在,求出所有滿足條件的F點坐標;如果不存在,請說明理由
(3)點K拋物線上C關于對稱軸的對稱點,點G拋物線上的動點,在x軸上是否存在點F,使A、K、F、G這樣的四個點為頂點的四邊形是平行四邊形?如果存在,求出所有滿足條件的F點坐標;如果不存在,請說明理由
(1) 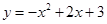 .
.
(2)存在,可證明DC⊥BC,由∠PBC+∠BDC=90°,知找一點P,使得∠PBC=∠DBC,故知P有兩個位置:(1,4)和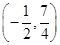
(3)存在4個這樣的點F,分別是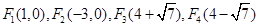
解析(1)拋物線的對稱軸:x=﹣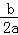 =﹣
=﹣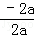 =1,且AB=4,則 A(﹣1,0)、B(3,0);
=1,且AB=4,則 A(﹣1,0)、B(3,0);
再代入點(2,3)后,可得: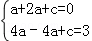 ,解得
,解得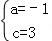
∴二次函數的表達式:y=﹣x2+2x+3.
(2)由(1)知:y=﹣x2+2x+3=﹣(x﹣1)2+4,則 D(1,4);
BC2=18、CD2=2、BD2=20,∴BC2+CD2=BD2,即△BCD是直角三角形,且DC⊥BC.
∴∠BDC+∠DBC=90°,即點D符合點P的要求,P1(1,4).
延長DC至E,使得DC=CE,則△BDE是等腰三角形,且∠DBC=∠EBC,則直線BE與拋物線的交點也符合點P的要求(B點除外)
通過圖示,不難看出點D、E關于點C對稱,則 E(﹣1,2),設直線BE:y=kx+b,則有: ,解得
,解得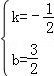
∴直線BE:y=﹣ x+
x+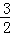 ,聯立拋物線的解析式后,得:
,聯立拋物線的解析式后,得: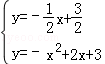 ,解得
,解得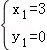 (舍)、
(舍)、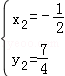
∴P2(﹣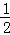 ,
,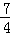 );
);
綜上,存在符合條件的點P,且坐標為(1,4)、(﹣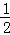 ,
,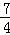 ).
).
(3)易知點K(2,3);
由題意,A、F都在x軸上,根據平行四邊形的特點不難看出點G的縱坐標為3或﹣3;
當yG=3時,﹣x2+2x+3=3,解得 x=0或2,
∴G點坐標為(0,3),
此時點F的坐標為(﹣1﹣2,0)或(﹣1+2,0),即(﹣3,0)、(1,0);
當yG=﹣3時,﹣x2+2x+3=﹣3,解得 x=1±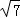 ,
,
∴G點坐標為(1+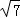 ,0)或(1﹣
,0)或(1﹣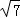 ,0),
,0),
此時點F的坐標為(4+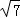 ,0)、(4﹣
,0)、(4﹣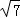 ,0);
,0);
綜上,有四個符合條件的點F,且坐標為(﹣3,0)、(1,0)、(4+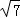 ,0)、(4﹣
,0)、(4﹣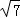 ,0).
,0).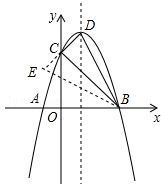


科目:初中數學 來源: 題型:
(本題滿分12分)在平面直角坐標系中,一次函數的圖象與坐標軸圍成的三角形,叫做此一次函數的坐標三角形.例如,圖中的一次函數的圖象與x,y軸分別交于點A,B,則△OAB為此函數的坐標三角形.
(1)求函數y=![]() x+3的坐標三角形的三條邊長;
x+3的坐標三角形的三條邊長;
(2)若函數y=![]() x+b(b為常數)的坐標三角形周長為16,求此三角形面積.
x+b(b為常數)的坐標三角形周長為16,求此三角形面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
(本題滿分12分)在平面直角坐標系xOy中,邊長為a(a為大于0的常數)的正方形ABCD的對角線AC、BD相交于點P,頂點A在x軸正半軸上運動,頂點B在y軸正半軸上運動(x軸的正半軸、y軸的正半軸都不包含原點O),頂點C、D都在第一象限。
(1)當∠BAO=45°時,求點P的坐標;
(2)求證:無論點A在x軸正半軸上、點B在y軸正半軸上怎樣運動,點P都在∠AOB的平分線上;
 (3)設點P到x軸的距離為h,試確定h的取值范圍,并說明理由。
(3)設點P到x軸的距離為h,試確定h的取值范圍,并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
(本題滿分12分)在平面直角坐標系中,一次函數的圖象與坐標軸圍成的三角形,叫做此一次函數的坐標三角形.例如,圖中的一次函數的圖象與x,y軸分別交于點A,B,則△OAB為此函數的坐標三角形.
(1)求函數y=![]() x+3的坐標三角形的三條邊長;
x+3的坐標三角形的三條邊長;
(2)若函數y=![]() x+b(b為常數)的坐標三角形周長為16,求此三角形面積.
x+b(b為常數)的坐標三角形周長為16,求此三角形面積.
查看答案和解析>>
科目:初中數學 來源:2011-2012年江蘇省揚州市九年級第一學期期末考試數學卷 題型:解答題
(本題滿分12分)在直角坐標系中,拋物線 經過點(0,10)
經過點(0,10)
和點(4,2).

1.(1) 求這條拋物線的函數關系式.
2.(2)如圖,在邊長一定的矩形ABCD中,CD=1,點C在y軸右側沿拋物線 滑動,在滑動過程中CD∥x軸,AB在CD的下方.當點D在y軸上時,AB正好落在x軸上.
滑動,在滑動過程中CD∥x軸,AB在CD的下方.當點D在y軸上時,AB正好落在x軸上.
①求邊BC的長.
②當矩形ABCD在滑動過程中被x軸分成兩部分的面
積比為1:4時,求點C的坐標.
查看答案和解析>>
科目:初中數學 來源:江蘇省蘇州市高新區2013屆七年級下學期期末考試數學試題 題型:解答題
(本題滿分12分)在平面直角坐標系 中,已知二次函數
中,已知二次函數 的圖象與x軸交于A,B兩點(點A在點B的左邊),AB=4,與y軸交于點C,且過點(2,3).
的圖象與x軸交于A,B兩點(點A在點B的左邊),AB=4,與y軸交于點C,且過點(2,3).
(1)求此二次函數的表達式;
(2)若拋物線的頂點為D,連接CD、CB,問拋物線上是否存在點P,使得∠PBC+∠BDC=90°. 若存在,求出點P的坐標;若不存在,請說明理由;
 (3)點K拋物線上C關于對稱軸的對稱點,點G拋物線上的動點,在x軸上是否存在點F,使A、K、F、G這樣的四個點為頂點的四邊形是平行四邊形?如果存在,求出所有滿足條件的F點坐標;如果不存在,請說明理由
(3)點K拋物線上C關于對稱軸的對稱點,點G拋物線上的動點,在x軸上是否存在點F,使A、K、F、G這樣的四個點為頂點的四邊形是平行四邊形?如果存在,求出所有滿足條件的F點坐標;如果不存在,請說明理由
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com