
【題目】已知兩個共一個頂點的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,連接AF,M是AF的中點,連接MB、ME.
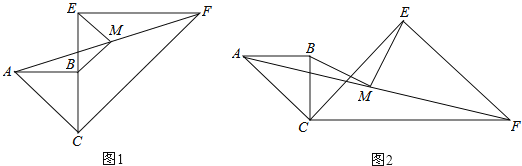
(1)如圖1,當CB與CE在同一直線上時,求證:MB∥CF;
(2)如圖1,若CB=a,CE=2a,求BM,ME的長;
(3)如圖2,當∠BCE=45°時,求證:BM=ME.
【答案】(1)證明見解析;(2)BM=ME=![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】
(1)如圖1,延長AB交CF于點D,證明BM為△ADF的中位線即可.
(2)如圖2,作輔助線,推出BM、ME是兩條中位線.
(3)如圖3,作輔助線,推出BM、ME是兩條中位線:BM=![]() DF,ME=
DF,ME=![]() AG;然后證明△ACG≌△DCF,得到DF=AG,從而證明BM=ME.
AG;然后證明△ACG≌△DCF,得到DF=AG,從而證明BM=ME.
(1)如圖1,延長AB交CF于點D,則易知△ABC與△BCD均為等腰直角三角形,
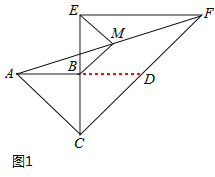
∴AB=BC=BD.
∴點B為線段AD的中點.
又∵點M為線段AF的中點,
∴BM為△ADF的中位線.
∴BM∥CF.
(2)如圖2,延長AB交CF于點D,則易知△BCD與△ABC為等腰直角三角形,
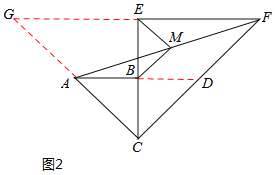
∴AB=BC=BD=a,AC=AD=![]() a,
a,
∴點B為AD中點,又點M為AF中點.
∴BM=![]() DF.
DF.
分別延長FE與CA交于點G,則易知△CEF與△CEG均為等腰直角三角形,
∴CE=EF=GE=2a,CG=CF=![]() a.
a.
∴點E為FG中點,又點M為AF中點.
∴ME=![]() AG.
AG.
∵CG=CF=![]() a,CA=CD=
a,CA=CD=![]() a,∴AG=DF=
a,∴AG=DF=![]() a.
a.
∴BM=ME=![]() .
.
(3)如圖3,延長AB交CE于點D,連接DF,則易知△ABC與△BCD均為等腰直角三角形,
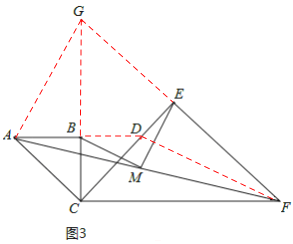
∴AB=BC=BD,AC=CD.
∴點B為AD中點.
又點M為AF中點,∴BM=![]() DF.
DF.
延長FE與CB交于點G,連接AG,則易知△CEF與△CEG均為等腰直角三角形,
∴CE=EF=EG,CF=CG.
∴點E為FG中點.
又點M為AF中點,∴ME=![]() AG.
AG.
在△ACG與△DCF中,∵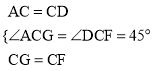 ,
,
∴△ACG≌△DCF(SAS).
∴DF=AG,∴BM=ME.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c與x軸交于點A(﹣1,0)和點B,化簡![]() 的結果為: ①c;②;③b﹣a;④a﹣b+2c.其中正確的有( )
的結果為: ①c;②;③b﹣a;④a﹣b+2c.其中正確的有( )
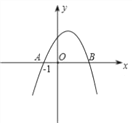
A. 一個 B. 兩個 C. 三個 D. 四個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古希臘著名的畢達哥拉斯學派把1,3,6,10…這樣的數稱為“三角形數”,而把1,4,9,16…這樣的數稱為“正方形數”.觀察下面的點陣圖和相應的等式,探究其中的規律:
(1)下圖反映了任何一個三角形數是如何得到的,認真觀察,并在④后面的橫線上寫出相應的等式;
![]()
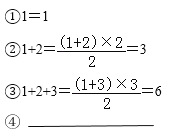
(2)通過猜想,寫出(1)中與第八個點陣相對應的等式 ;
(3)從下圖中可以發現,任何一個大于1的“正方形數”都可以看作兩個相鄰“三角形數”之和.結合(1)觀察下列點陣圖,并在⑤看面的橫線上寫出相應的等式.


(4)通過猜想,寫出(3)中與第n個點陣相對應的等式 ;
(5)判斷256是不是正方形數,如果不是,說明理由;如果是,256可以看作哪兩個相鄰的“三角形數”之和?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線![]() 與⊙O,AB是⊙O的直徑,AD⊥
與⊙O,AB是⊙O的直徑,AD⊥![]() 于點D.
于點D.
(1)如圖①,當直線![]() 與⊙O相切于點C時,若∠DAC=30°,求∠BAC的大小;
與⊙O相切于點C時,若∠DAC=30°,求∠BAC的大小;
(2)如圖②,當直線![]() 與⊙O相交于點E、F時,若∠DAE=18°,求∠BAF的大小.
與⊙O相交于點E、F時,若∠DAE=18°,求∠BAF的大小.
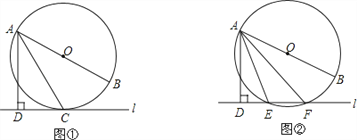
查看答案和解析>>
科目:初中數學 來源: 題型:
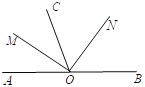
【題目】如圖,O為直線AB上一點,OM是∠AOC的角平分線,ON是∠COB的平分線
(1)指出圖中所有互為補角的角,
(2)求∠MON的度數,
(3)指出圖中所有互為余角的角.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學八年級組織了一次“漢字聽寫比賽”,每班選25名同學參加比賽,成績分為A,B,C,D四個等級,其中A等級得分為100分,B等級得分為85分,C等級得分為75分,D等級得分為60分,語文教研組將八年級一班和二班的成績整理并繪制成如下的統計圖,請根損換供的信息解答下列問題.
(1)把一班比賽成統計圖補充完整;

(2)填表:
平均數(分) | 中位數(分) | 眾數(分) | |
一班 | a | b | 85 |
二班 | 84 | 75 | c |
表格中:a=______,b=______,c=_______.
(3)請從以下給出的兩個方面對這次比賽成績的結果進行分析:
①從平均數、眾數方面來比較一班和二班的成績;
②從B級以上(包括B級)的人數方面來比較-班和二班的成績.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出如下定義:如果兩個不相等的有理數a,b滿足等式a-b=ab.那么稱a,b是“關聯有理數對”,記作(a,b).如:因為![]() ,
,![]() .所以數對(3,
.所以數對(3,![]() )是“關聯有理數對”.
)是“關聯有理數對”.
(1)在數對①(1,![]() )、②(-1,0)、③(
)、②(-1,0)、③(![]() ,
,![]() )中,是“關聯有理數對”的是____________(只填序號);
)中,是“關聯有理數對”的是____________(只填序號);
(2)若(m,n)是“關聯有理數對”,則(-m,-n)___________“關聯有理數對”(填“是”或“不是”);
(3)如果兩個有理數是一對“關聯有理數對”,其中一個有理數是5,求另一個有理數.
查看答案和解析>>
科目:初中數學 來源: 題型:
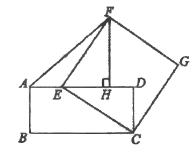
【題目】如圖,在矩形ABCD中,AD=4,點E在邊AD上,連接CE,以CE為邊向右上方作正方形CEFG,作FH⊥AD,垂足為H,連接AF.
(1)求證:FH=ED;
(2)當AE為何值時,△AEF的面積最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com