
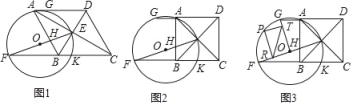
【題目】已知四邊形ABCD是菱形,AC、BD交于點E,點F在CB的延長線上,連結EF交AB于H,以EF為直徑作⊙O,交直線AD于A、G兩點,交BC于K點.
(1)如圖1,連結AF,求證:四邊形AFBD是平行四邊形;
(2)如圖2,當∠ABC=90°時,求tan∠EFC的值;
(3)如圖3,在(2)的條件下,連結OG,點P在弧FG上,過點P作PT∥OF交OG于T,PR∥OG交OF于R點,連結TR,若AG=2,在點P運動過程中,探究線段TR的長是否為定值,如果是,則求出這個定值;如果不是,請說明理由.
【答案】(1)詳見解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)連接AF,由EF是⊙O的直徑知FA⊥AC,由四邊形ABCD是菱形知BD⊥AC、AD∥FB,據此可得FA∥BD,即可得證;
(2)連接EK,先證四邊形ABCD是正方形,由EF是⊙O的直徑知FK⊥EK,設BK=EK=a,則BC=AD=FB=2a,根據tan∠EFC=![]() 可得答案;
可得答案;
(3)連接OP、FA,過點O作OM⊥GD,并延長MO交FC于點N,先證四邊形PROT是矩形得RT=OP=OG,由MN⊥FC知tan∠EFC=tan∠GOM=![]() ,由AG=2、OM⊥GD知GM=1、OM=3,由勾股定理可得GO=
,由AG=2、OM⊥GD知GM=1、OM=3,由勾股定理可得GO=![]() ,繼而可得答案.
,繼而可得答案.
(1)如圖1,連接AF,

∵EF是⊙O的直徑,
∴∠FAC=90°,即FA⊥AC,
∵四邊形ABCD是菱形,
∴BD⊥AC,AD∥BC、即AD∥FB,
∴FA∥BD,
∴四邊形AFBD是平行四邊形;
(2)如圖2,連接EK,
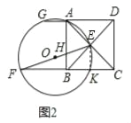
∵∠ABC=90°,四邊形ABCD是菱形,
∴四邊形ABCD是正方形,
∵EF是⊙O的直徑,
∴FK⊥EK,
設BK=EK=a,則BC=AD=FB=2a,
則tan∠EFC=![]() =
=![]() ;
;
(3)TR的長是定值,
如圖3,連接OP、FA,過點O作OM⊥GD,并延長MO交FC于點N,

∵EF是⊙O的直徑,
∴FA⊥EA,
又∵四邊形ABCD是正方形,
∴∠BAC=45°,
∴∠GAF=45°,
∴∠GOF=90°,
∵PT∥OF、PR∥OG,
∴四邊形PROT是矩形,
∴RT=OP=OG,
∵OM⊥GD、GD∥FC,
∴MN⊥FC,
∴tan∠EFC=tan∠GOM=![]() ,
,
∵AG=2、OM⊥GD,
∴GM=1,
∴OM=3,
由勾股定理可得GO=![]() ,
,
∴RT=![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
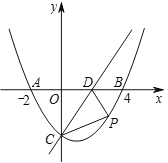
【題目】如圖,在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() ,與直線
,與直線![]() 交于點
交于點![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() .
.
(1)求該拋物線的解析式.
(2)點![]() 是拋物線上第四象限上的一個動點,連接
是拋物線上第四象限上的一個動點,連接![]() ,
,![]() ,當
,當![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標.
的坐標.
(3)將拋物線的對稱軸向左平移3個長度單位得到直線![]() ,點
,點![]() 是直線
是直線![]() 上一點,連接
上一點,連接![]() ,
,![]() ,若直線
,若直線![]() 上存在使
上存在使![]() 最大的點
最大的點![]() ,請直接寫出滿足條件的點
,請直接寫出滿足條件的點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校九年級男生200米跑的水平,從中隨機抽取部分男生進行測試,并把測試成績分為D、C、B、A四個等次繪制成如圖所示的不完整的統計圖,請你依圖解答下列問題:
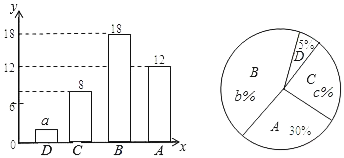
(1)a= ,b= ,c= ;
(2)扇形統計圖中表示C等次的扇形所對的圓心角的度數為 度;
(3)學校決定從A等次的甲、乙、丙、丁四名男生中,隨機選取兩名男生參加全市中學生200米跑比賽,請用列表法或畫樹狀圖法,求甲、乙兩名男生同時被選中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
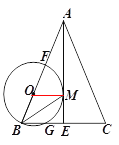
【題目】如圖,在△ABC中,AB=AC,AE是BC邊上的高線,BM平分∠ABC交AE于點M,經過B,M 兩點的⊙O交BC于點G,交AB于點F ,FB為⊙O的直徑.
(1)求證:AM是⊙O的切線
(2)當BE=3,cosC=![]() 時,求⊙O的半徑.
時,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
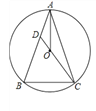
【題目】如圖,△ABC內接于⊙O,AB=AC,CO的延長線交AB于點D.
(1)求證:AO平分∠BAC;
(2)若BC=6,sin∠BAC=![]() ,求AC和CD的長.
,求AC和CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
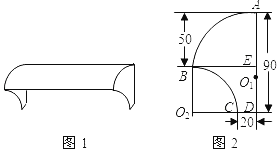
【題目】小帥家的新房子剛裝修完,便遇到罕見的大雨,于是他向爸爸提議給窗戶安上遮雨罩.如圖1所示的是他了解的一款雨罩.它的側面如圖2所示,其中頂部圓弧AB的圓心O在整直邊緣D上,另一條圓弧BC的圓心O.在水平邊緣DC的廷長線上,其圓心角為90°,BE⊥AD于點E,則根據所標示的尺寸(單位:c)可求出弧AB所在圓的半徑AO的長度為_____cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為增強學生體質,各學校普遍開展了陽光體育活動,某校為了解全校1000名學生每周課外體育活動時間的情況,隨機調查了其中的50名學生,對這50名學生每周課外體育活動時間x(單位:小時)進行了統計.根據所得數據繪制了一幅不完整的統計圖,并知道每周課外體育活動時間在6≤x<8小時的學生人數占24%.根據以上信息及統計圖解答下列問題:
(1)本次調查屬于 調查,樣本容量是 ;
(2)請補全頻數分布直方圖中空缺的部分;
(3)求這50名學生每周課外體育活動時間的平均數;
(4)估計全校學生每周課外體育活動時間不少于6小時的人數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com