
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 開始沿邊
開始沿邊![]() 向點
向點![]() 以每秒1個單位長度的速度運動,動點
以每秒1個單位長度的速度運動,動點![]() 從點
從點![]() 開始沿邊
開始沿邊![]() 向點
向點![]() 以每秒2個單位長度的速度運動,過點
以每秒2個單位長度的速度運動,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .點
.點![]() 分別從點
分別從點![]() 同時出發,當其中一點到達終點時,另一點也隨之停止運動,設運動時間為
同時出發,當其中一點到達終點時,另一點也隨之停止運動,設運動時間為![]() 秒
秒![]() .
.
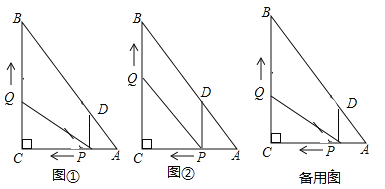
(1)如圖①,直接用含![]() 的代數式分別表示:
的代數式分別表示:![]() ,
,![]() ______,
______,
(2)如圖②,
①當![]() _____秒時,四邊形
_____秒時,四邊形![]() 為平行四邊形.
為平行四邊形.
②是否存在![]() 的值,使四邊形
的值,使四邊形![]() 為菱形?若存在,寫出
為菱形?若存在,寫出![]() 的值;若不存在,請求出當點
的值;若不存在,請求出當點![]() 的速度(勻速運動)變為每秒多少個單位長度時,才能使四邊形
的速度(勻速運動)變為每秒多少個單位長度時,才能使四邊形![]() 在某一時刻成為菱形?
在某一時刻成為菱形?
(3)設![]() 的外接圓面積為
的外接圓面積為![]() ,求出
,求出![]() 與
與![]() 的函數關系式,并判斷當
的函數關系式,并判斷當![]() 最小時,
最小時,![]() 的外接圓與直線
的外接圓與直線![]() 的位置關系,并且說明理由.
的位置關系,并且說明理由.
【答案】(1)![]() ;
;![]() ;(2)①
;(2)①![]() ,②不存在菱形,詳見解析;(3)
,②不存在菱形,詳見解析;(3)![]() 的外接圓與直線
的外接圓與直線![]() 相交.詳見解析
相交.詳見解析
【解析】
(1)根據題意得到CQ=2t,AP=t,求出BQ,證明△ADP∽△ABC,根據相似三角形的性質求出PD;
(2)①根據平行四邊形的判定方法列出關于t的方程,解方程即可;
②根據菱形的判定方法列出關于t的方程,解方程,看是否符合題意;
(3)![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,由勾股定理找到
,由勾股定理找到![]() 與
與![]() 的函數關系式,并求得S最小時,t的值,從而求出OM的長,再判斷圓與直線的位置關系.
的函數關系式,并求得S最小時,t的值,從而求出OM的長,再判斷圓與直線的位置關系.
(1)由題意得,CQ=2t,AP=t,
則BQ=8-2t,
∵DP⊥AC,BC⊥AC,
∴PD∥BC,
∴△ADP∽△ABC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得PD=![]()
故答案為:8-2t;![]() ;
;
(2)①∵PD∥BC,
∴當PD=BQ時,四邊形PDBQ為平行四邊形,
∴8-2t=![]()
解得t=![]() ,
,
則當t=![]() 時,四邊形PDBQ為平行四邊形;
時,四邊形PDBQ為平行四邊形;
②不存在菱形,
設點![]() 的速度為每秒
的速度為每秒![]() 個單位長度.
個單位長度.
則![]() ,
,![]() ,
,![]() .
.
要使四邊形![]() 是菱形,則
是菱形,則![]() .
.
當![]() ,即
,即![]() .解得
.解得![]() .
.
當![]() ,
,![]() 時,即
時,即![]() ,解得
,解得![]() .
.
∴當點![]() 的速度為每秒
的速度為每秒![]() 個單位時,經過
個單位時,經過![]() 秒,四邊形
秒,四邊形![]() 是菱形.
是菱形.
(3)如圖,![]() 是
是![]() 的外接圓的圓心,作
的外接圓的圓心,作![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,連接
,連接![]() 、
、![]() 、
、![]() .
.
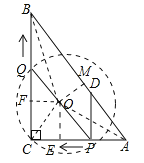
∵![]()
∴![]() ;
;
∴![]() 時,
時,![]() 取最小值.
取最小值.
此時![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的外接圓與直線
的外接圓與直線![]() 相交.
相交.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+4交y軸于點A,交過點A且平行于x軸的直線于另一點B,交x軸于C,D兩點(點C在點D右邊),對稱軸為直線x=![]() ,連接AC,AD,BC.若點B關于直線AC的對稱點恰好落在線段OC上,下列結論中錯誤的是( )
,連接AC,AD,BC.若點B關于直線AC的對稱點恰好落在線段OC上,下列結論中錯誤的是( )
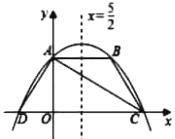
A.點B坐標為(5,4)B.AB=ADC.a=![]() D.OCOD=16
D.OCOD=16
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小騰的爸爸計劃將一筆資金用于不超過10天的短期投資,針對這筆資金,銀行專屬客戶經理提供了三種投資方案,這三種方案的回報如下:
方案一:每一天回報30元;
方案二:第一天回報8元,以后每一天比前一天多回報8元;
方案三:第一天回報0.5元,以后每一天的回報是前一天的2倍.
下面是小騰幫助爸爸選擇方案的探究過程,請補充完整:
(1)確定不同天數所得回報金額(不足一天按一天計算),如下表:
天數 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
方案一 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
方案二 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
方案三 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
|
其中![]() ________;
________;
(2)計算累計回報金額,設投資天數為![]() (單位:天),所得累計回報金額是
(單位:天),所得累計回報金額是![]() (單位:元),于是得到三種方案的累計回報金額
(單位:元),于是得到三種方案的累計回報金額![]() ,
,![]() ,
,![]() 與投資天數
與投資天數![]() 的幾組對應值:
的幾組對應值:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
| 8 | 24 | 48 | 80 | 120 | 168 | 224 | 288 | 360 | 440 |
| 0.5 | 1.5 | 3.5 | 7.5 | 15.5 | 31.5 | 63.5 | 127.5 | 255.5 |
|
其中![]() ________;
________;
(3)在同一平面直角坐標系![]() 中,描出補全后的表中各組數值所對應的點
中,描出補全后的表中各組數值所對應的點![]() ,
,![]() ,
,![]() ,并畫出
,并畫出![]() ,
,![]() ,
,![]() 的圖象;
的圖象;
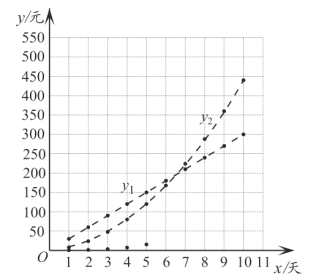
注:為了便于分析,用虛線連接離散的點.
(4)結合圖象,小騰給出了依據不同的天數而選擇對應方案的建議:
_________________________________________________________________________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售10臺A型和20臺B型加濕器的利潤為2500元,銷售20臺A型和10臺B型加濕器的利潤為2000元
(1)求每臺A型加濕器和B型加濕器的銷售利潤;
(2)該商店計劃一次購進兩種型號的加濕器共100臺,其中B型加濕器的進貨量不超過A型加濕器的2倍,設購進A型加濕器x臺.這100臺加濕器的銷售總利潤為y元
①求y關于x的函數關系式;
②該商店應怎樣進貨才能使銷售總利潤最大?
(3)實際進貨時,廠家對A型加濕器出廠價下調m(0<m<100)元,且限定商店最多購進A型加濕器70臺,若商店保持兩種加濕器的售價不變,請你根據以上信息及(2)中條件,設計出使這100臺加濕器銷售總利潤最大的進貨方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級有學生400人,為了解這個年級普及安全教育的情況,隨機抽取了20名學生,進行安全教育考試,測試成績(百分制)如下:
71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
(1)請補全七年級20名學生安全教育測試成績頻數分布直方圖;
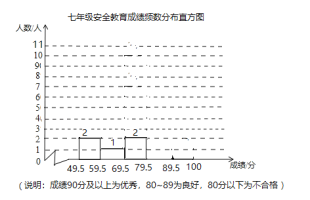
(2)樣本數據的平均數、中位數、眾數、優秀率如下表所示,請補充完整;
年級 | 平均數 | 中位數 | 眾數 | 優秀率 |
七年級 | 85.4 |
|
|
|
(3)估計七年級成績優秀的學生人數約為_________人.
(4)學校有安全教育老師男女各2名,現從這4名老師中隨機挑選2名參加“安全教育”宣傳活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一大、一小兩個等腰直角三角形拼在一起,![]() ,連接
,連接![]() .
.
(1)如圖1,若![]() 三點在同一條直線上,則
三點在同一條直線上,則![]() 與
與![]() 的關系是 ;
的關系是 ;
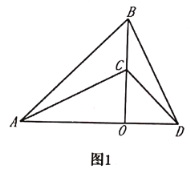
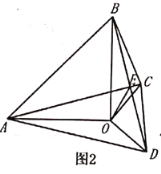
(2)如圖2,若![]() 三點不在同一條直線上,
三點不在同一條直線上,![]() 與
與![]() 相交于點
相交于點![]() ,連接
,連接![]() ,猜想
,猜想![]() 之間的數量關系,并給予證明;
之間的數量關系,并給予證明;
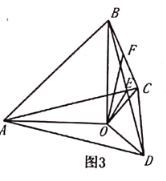
(3)如圖3,在(2)的條件下作![]() 的中點
的中點![]() ,連接
,連接![]() ,直接寫出
,直接寫出![]() 與
與![]() 之間的關系.
之間的關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小明同學設計的“過直線外一點作已知直線的平行線“的尺規作圖過程.

已知:如圖,直線![]() 和直線
和直線![]() 外一點
外一點![]() .
.
求作:直線![]() ,使直線
,使直線![]() 直線
直線![]() .
.
作法:如圖,
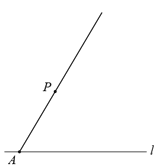
①在直線![]() 上任取一點
上任取一點![]() ,作射線
,作射線![]() ;
;
②以![]() 為圓心,
為圓心,![]() 為半徑作弧,交直線
為半徑作弧,交直線![]() 于點
于點![]() ,連接
,連接![]() ;
;
③以![]() 為圓心,
為圓心,![]() 長為半徑作弧,交射線
長為半徑作弧,交射線![]() 于點
于點![]() ;分別以
;分別以![]() 為圓心,大于
為圓心,大于![]() 長為半徑作弧,在
長為半徑作弧,在![]() 的右側兩弧交于點
的右側兩弧交于點![]() ;
;
④作直線![]() ;
;
所以直線![]() 就是所求作的直線.
就是所求作的直線.
根據上述作圖過程,回答問題:
(1)用直尺和圓規,補全圖中的圖形;
(2)完成下面的證明:
證明:由作圖可知![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() .(_______________________________)(填依據1).
.(_______________________________)(填依據1).
![]() ,
,
![]() .
.
![]() ,∴直線
,∴直線![]() 直線
直線![]() .(______________________)(填依據2).
.(______________________)(填依據2).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市教育行政部門為了解初中學生參加綜合實踐活動的情況,隨機抽取了本市初一、初二、初三年級各![]() 名學生進行了調查,調查結果如圖所示,請你根據圖中的信息回答問題.
名學生進行了調查,調查結果如圖所示,請你根據圖中的信息回答問題.

(1)在被調查的學生中,參加綜合實踐活動的有多少人,參加科技活動的有多少人;
(2)如果本市有![]() 萬名初中學生,請你估計參加科技活動的學生約有多少名.
萬名初中學生,請你估計參加科技活動的學生約有多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某養殖場計劃今年養殖無公害標準化龍蝦和鯉魚,由于受養殖水面的制約,這兩個品種的苗種的總投放量只有50噸.根據經驗測算,這兩個品種的種苗每投放一噸的先期投資、養殖期間的投資以及產值如下表:(單位:千元/噸)
品種 | 先期投資 | 養殖期間投資 | 產值 |
鯉魚 | 9 | 3 | 30 |
龍蝦 | 4 | 10 | 20 |
養殖場受經濟條件的影響,先期投資不超過360千元,養殖期間的投資不超過290千元.設鯉魚種苗的投放量為x噸.
(1)求x的取值范圍;
(2)設這兩個品種產出后的總產值為y(千元),試寫出y與x之間的函數關系式,并求出當x等于多少時,y有最大值?最大值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com