Question

如圖，矩形OABC在平面直角坐標系中，O為坐標原點，點A（0，4），C（2，0），將矩形OABC繞點O按順時針方向旋轉135⁰，得到矩形EFGH（點E與O重合）.

（1）若GH交y軸于點M，則∠FOM＝      ，OM=        ；
（2）矩形EFGH沿y軸向上平移t個單位.
①直線GH與x軸交于點D，若AD∥BO，求t的值；
②若矩形EFHG與矩形OABC重疊部分的面積為S個平方單位，試求當0<t≤時，S與t之間的函數關系式.

Answer 1

（1）45⁰，；（2）①－2；②.

解析試題分析：（1）由旋轉的性質，得∠AOF＝135⁰，∴∠FOM＝45⁰，由旋轉的性質，得∠OHM＝45⁰，OH=OC=2，∴OM=；（2）①由矩形的性質和已知AD∥BO，可得四邊形ABOD是平行四邊形，從而DO=AB=2，又由△DOI是等腰直角三角形可得OI=OD=2，從而由平移的性質可求得t=IM=OM－OI=－2；②首先確定當0<t≤時，矩形EFGH沿y軸向上平移過程中關鍵點的位置，分0<t≤2，2<t≤， <t≤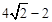三種情況求出S與t之間的函數關系式.
試題解析：（1）45⁰；.
（2）①如圖1，設直線HG與y軸交于點I，
∵四邊形OABC是矩形，∴AB∥DO，AB=OC.
∵C（2，0），∴AB=OC=2.
又∵AD∥BO， ∴四邊形ABOD是平行四邊形. ∴DO=AB=2.
由（1）易得，△DOI是等腰直角三角形，∴OI=OD=2.
∴t=IM=OM－OI=－2.

②如圖2，

過點F，G分別作x軸，y軸的垂線，垂足為R，T，連接OC. 則
由旋轉的性質，得，OF=OA=4，∠FOR＝45⁰，
∴OR=RF=，F（，－）.
由旋轉的性質和勾股定理，得OG=，
設TG=MT=x，則OT=OM＋MT=.
在Rt△OTG中，由勾股定理，得，解得x=. ∴G（，－）.
∴用待定系數法求得直線FG的解析式為.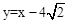
當x=2時，.
∴當t=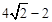時，就是GF平移到過點C時的位置（如圖5）.
∴當0<t≤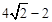時，幾個關鍵點如圖3，4，5所示：
如圖3 ，t=OE=OC=2，此時，矩形EFGH沿y軸向上平移過程中邊EF經過點C；

如圖4，t=OE=OM=，此時，矩形EFGH沿y軸向上平移過程中邊HG經過點O；

如圖5，t=OE=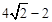，此時，矩形EFGH沿y軸向上平移過程中邊FG經過點C.

∴（Ⅰ）當0<t≤2時，矩形EFHG與矩形OABC重疊部分的面積為△OCS的面積（如圖6）.此時，OE="OS=" t， ∴.

（Ⅱ）當2<t≤時，矩形EFHG與矩形OABC重疊部分的面積為直角梯形OEPC的面積（如圖7）.此時OE= t，，OC=2.

由E（0，t），∠FFO=45⁰，用用待定系數法求得直線EP的解析式為.
當x=2時，. ∴CP=. ∴.
（Ⅲ）當<t≤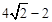時，矩形EFHG與矩形OABC重疊部分的面積為五邊形EQCUV的面積（如圖8），

它等于直角梯形EQCO的面積減去直角三角形VOU的的面積.
此時，OE= t，，OC=2，CQ= ，OU="OV=" t－.
∴.
綜上所述，當0<t≤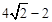時，S與t之間的函數關系式為.
考點：1.旋轉的性質；2.矩形的性質；3.勾股定理；4.平移的性質；5.平行四邊形的判定和性質；6.等腰直角三角形的判定和性質；7.待定系數法；8.直線上點的坐標與方程的關系；9.分類思想的應用.