
【題目】已知y是x的一次函數,且當x=﹣4時,y=9;當x=6時,y=﹣1.
(1)求這個一次函數的解析式;
(2)當x=﹣ ![]() 時,函數y的值;
時,函數y的值;
(3)當y<1時,自變量x取值范圍.
【答案】
(1)解:設這個一次函數的解析式為y=kx+b(k≠0),
把(﹣4,9)、(6,﹣1)代入y=kx+b中,
![]() ,解得:
,解得: ![]() ,
,
∴這個一次函數的解析式為y=﹣x+5
(2)解:當x=﹣ ![]() 時,y=﹣(﹣
時,y=﹣(﹣ ![]() )+5=
)+5= ![]() .
.
(3)解:∵y=﹣x+5<1,
∴x>4
【解析】(1)設這個一次函數的解析式為y=kx+b(k≠0),根據點的坐標利用待定系數法即可求出一次函數解析式;(2)將x=﹣ ![]() 代入一次函數解析式中求出y值即可;(3)由y<1可得出關于x的一元一次不等式,解之即可得出結論.
代入一次函數解析式中求出y值即可;(3)由y<1可得出關于x的一元一次不等式,解之即可得出結論.
【考點精析】本題主要考查了一次函數的性質和確定一次函數的表達式的相關知識點,需要掌握一般地,一次函數y=kx+b有下列性質:(1)當k>0時,y隨x的增大而增大(2)當k<0時,y隨x的增大而減小;確定一個一次函數,需要確定一次函數定義式y=kx+b(k不等于0)中的常數k和b.解這類問題的一般方法是待定系數法才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】若將一個自然數各位上的數字按照從高位數字到低位數字排成一列后,后一個人數減去前一個數的差是一個常數,則這個數叫做“幸福數”.如:四位數2468排成一列后為:2,4,6,8.因為8-6=6-4=4-2=2,且差為2的常數,故2468是一個差為2的四位“幸福數”.又如,9876,6666等也是“幸福數”.
若一個自然數從左到右各數位上的數字和另一個自然數從右到左各數位上的數字完全相同,則稱這兩個數為“三生三世數”.例如:3579與9753,8765與5678,...,都是“三生三世數”.
規定:把高位數字為x,差為2的三位“幸福數”與它的“三生三世數”的和與222的商記為F(x).例如當x=5時,三位“幸福數”為579,它的“三生三世數”為975,三位“幸福數”與它的“三生三世數”的和為:579+975=1554,1554÷222=7,所以F(x)=7.
(1)計算:F(1), F(4);
(2)已知F(x) =4,求x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一副直角三角板按圖11-14擺放,點C在EF上,AC經過點D.已知∠A=∠EDF=90°,AB=AC,∠E=30°,∠BCE=40°.求∠CDF的度數.
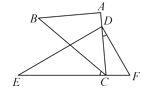
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:已知點P(x0,y0)和直線y=kx+b,則點P到直線y=kx+b的距離,可用公式d=![]() 計算.
計算.
例如:求點P(﹣1,2)到直線y=3x+7的距離.
解:因為直線y=3x+7,其中k=3,b=7.
所以點P(﹣1,2)到直線y=3x+7的距離為:d=![]() =
=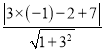 =
=![]() =
=![]() .
.
根據以上材料,解答下列問題:
(1)求點P(1,﹣1)到直線y=x﹣1的距離;
(2)已知⊙Q的圓心Q坐標為(0,5),半徑r為2,判斷⊙Q與直線y=![]() x+9的位置關系并說明理由;
x+9的位置關系并說明理由;
(3)已知直線y=﹣2x+4與y=﹣2x﹣6平行,求這兩條直線之間的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,射線OC在∠AOB的內部,圖中共有3個角:∠AOB,∠AOC和∠BOC,若其中有一個角的度數是另一個角度數的兩倍,則稱射線OC是∠AOB的“巧分線”.如圖2,若∠MPN=60°,且射線PQ繞點P從PN位置開始,以每秒10°的速度逆時針旋轉,當PQ與PN成180°時停止旋轉,旋轉的時間為t秒.若射線PM同時繞點P以每秒5°的速度逆時針旋轉,并與PQ同時停止,當t=____秒,射線PQ是∠MPN的“巧分線”.
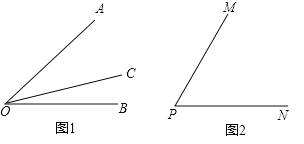
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com