
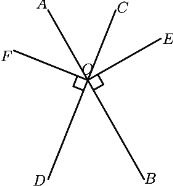
【題目】已知:如圖直線![]() 與
與![]() 相交于點
相交于點![]() ,
,![]()
(1)圖中與![]() 互余的角有 ,圖中與
互余的角有 ,圖中與![]() 互補的角有 (備注:寫出所有符合條件的角)
互補的角有 (備注:寫出所有符合條件的角)
(2)根據(jù)下列條件,分別求![]() 的度數(shù):①射線
的度數(shù):①射線![]() 平分
平分![]() ;②
;②![]()
【答案】(1)![]() ;
;![]() ;(2)①135°;②144°
;(2)①135°;②144°
【解析】
(1)若兩個角的和是90°,則稱這兩個角互為余角,根據(jù)題意與∠AOF互為余角的有∠AOC、∠BOD,若兩個角的和是180°,則稱這兩個角互為補角,根據(jù)題意與∠COE互為補角的有∠EOD、∠BOF.
(2)①射線![]() 平分
平分![]() 時,∠FOA=∠AOC=45°,根據(jù)對頂角∠COA=∠DOB=45°,從而得出∠FOE的度數(shù)②假設∠AOC=x,則∠FOE=4x,∠COA=∠DOB=x,根據(jù)題意列出方程即可求解.
時,∠FOA=∠AOC=45°,根據(jù)對頂角∠COA=∠DOB=45°,從而得出∠FOE的度數(shù)②假設∠AOC=x,則∠FOE=4x,∠COA=∠DOB=x,根據(jù)題意列出方程即可求解.
解:(1)∵![]()
∴∠FOD=∠EOB=90°
∵∠AOC與∠DOB是對頂角
∴∠COA=∠DOB
∵∠AOC+∠AOF+∠FOD=180°
∴∠AOC+∠AOF=90°
∴∠AOC和∠AOF互余,∠DOB和∠AOF互余
∵∠EOD+∠COE=180°,∠COE+∠FOB=180°
∴∠EOD和∠COE互補,∠COE和∠FOB互補
(2)①∵射線OA平分∠COF時,
∴2∠FOA=2∠AOC=90°
∴∠FOA=∠AOC=45°
∵∠AOC+∠COE=90°
∴∠COE=45°
∴∠EOF=135°
②當![]() 時
時
設∠AOC=x,則∠EOF=4x,∠DOB=x
∵∠EOF+∠DOB=180°
∴x+4x=180°
解的:x=36°
∴∠EOF=36°×4=144°


 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,四邊形ABCD是邊長為6的正方形,點E在邊AB上,BE=4,過點E作EF∥BC,分別交BD,CD于G,F兩點.若M,N分別是DG,CE的中點,則MN的長為( )

A. 3 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
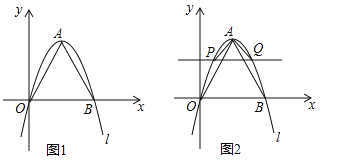
【題目】(2016吉林省)如圖1,在平面直角坐標系中,點B在x軸正半軸上,OB的長度為2m,以OB為邊向上作等邊三角形AOB,拋物線l:![]() 經(jīng)過點O,A,B三點.
經(jīng)過點O,A,B三點.
(1)當m=2時,a= ,當m=3時,a= ;
(2)根據(jù)(1)中的結果,猜想a與m的關系,并證明你的結論;
(3)如圖2,在圖1的基礎上,作x軸的平行線交拋物線l于P、Q兩點,PQ的長度為2n,當△APQ為等腰直角三角形時,a和n的關系式為 ;
(4)利用(2)(3)中的結論,求△AOB與△APQ的面積比.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】去年11月,體質監(jiān)測中心有關專家隨機抽查了我市若干名初中學生坐姿、站姿、走姿的好壞情況.我們對專家的測評數(shù)據(jù)作了適當處理(如果一個學生有一種以上不良姿勢,我們以他最突出的一種作記載),并將統(tǒng)計結果繪制了如下兩幅不完整的統(tǒng)計圖,請你根據(jù)圖中所給信息解答下列問題:
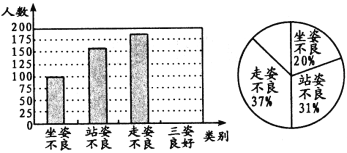
(1)請將兩幅統(tǒng)計圖補充完整;
(2)一共抽查了多少名學生?
(3)如果我市有10萬名初中生,那么我市初中生中,三姿良好的學生約有多少人?
(4)根據(jù)統(tǒng)計結果,請你簡單談談自己的看法.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
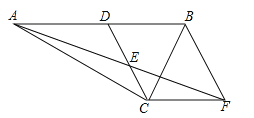
【題目】已知:如圖,在Rt△ACB中,∠ACB=90°,點D是AB的中點,點E是CD的中點,過點C作CF∥AB叫AE的延長線于點F.
(1)求證:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中, △ABC的三個頂點的位置如圖所示,點A'的坐標是
(-2,2), 現(xiàn)將△ABC平移,使點A變換為點A',點B′、C′分別是B、C的對應點。

(1)請畫出平移后的像△A'B'C'(不寫畫法) ,并直接寫出點B′、C′的坐標:
B′ ( ) 、C′ ( ) ;
(2)若△ABC 內部一點P的坐標為(a,b),則點P 的對應點P ′的坐標是 ( ) .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】珠江流域某江段江水流向經(jīng)過B、C、D三點拐彎后與原來相同,如圖,若∠ABC=120°,∠BCD=80°,則∠CDE=__________度.

(第22題)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
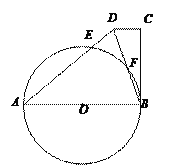
【題目】如圖,在四邊形ABCD中,AB=AD,∠C=90°,以AB為直徑的⊙O交AD于點E,CD=ED,連接BD交⊙O于點F.
(1)求證:BC與⊙O相切;
(2)若BD=10,AB=13,求AE的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】我市在各校推廣大閱讀活動,初二(1)班為了解2月份全班學生課外閱讀的情況,調查了全班學生2月份讀書的冊數(shù),并根據(jù)調查結果繪制了如下不完整的條形統(tǒng)計圖和扇形統(tǒng)計圖:
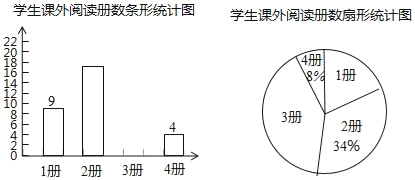
根據(jù)以上信息解決下列問題:
(1)參加本次問卷調查的學生共有 人,其中2月份讀書2冊的學生有 人;
(2)補全條形統(tǒng)計圖,并求扇形統(tǒng)計圖中讀書3冊所對應扇形的圓心角度數(shù);
(3)在讀書4冊的學生中恰好有2名男生和2名女生,現(xiàn)要在這4名學生中隨機選取2名學生參加學校的閱讀分享沙龍,請用列舉法(畫樹狀圖或列表)求所選取的這2名學生恰好性別相同的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com