
【題目】如圖,拋物線y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() 與x軸交于A,B兩點(A點在B點的左側),與y軸交于點C,已知點D(0,﹣
與x軸交于A,B兩點(A點在B點的左側),與y軸交于點C,已知點D(0,﹣ ![]() ).
).
(1)求直線AC的解析式;
(2)如圖1,P為直線AC上方拋物線上的一動點,當△PBD面積最大時,過P作PQ⊥x軸于點Q,M為拋物線對稱軸上的一動點,過M作y軸的垂線,垂足為點N,連接PM,NQ,求PM+MN+NQ的最小值;
(3)在(2)問的條件下,將得到的△PBQ沿PB翻折得到△PBQ′,將△BPQ′沿直線BD平移,記平移中的△PBQ′為△P′B′Q″,在平移過程中,設直線P′B′與x軸交于點E.則是否存在這樣的點E,使得△B′EQ″為等腰三角形?若存在,求此時OE的長.
【答案】
(1)解:∵拋物線y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() 與x軸交于A,B兩點(A點在B點的左側),與y軸交于點C,
與x軸交于A,B兩點(A點在B點的左側),與y軸交于點C,
∴A(﹣4,0),B(1,0),C(0, ![]() ),
),
設直線AC的解析式為y=kx+b,則有 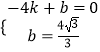 ,
,
∴k= ![]() ,b=
,b= ![]() ,
,
∴直線AC的解析式為y= ![]() x+
x+ ![]()
(2)解:如圖1中,分別過D、B作x軸,y軸的平行線交于點K,連接PK.設P(m,﹣ ![]() m2﹣
m2﹣ ![]() m+
m+ ![]() ).
).
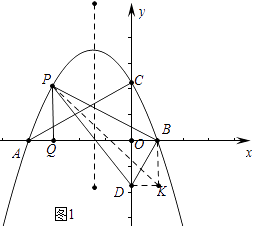
S△PDB=S△PDK+S△PBK﹣S△DKB
= ![]() 1(﹣
1(﹣ ![]() m2﹣
m2﹣ ![]() m+
m+ ![]() +
+ ![]() )+
)+ ![]()
![]() (1﹣m)﹣
(1﹣m)﹣ ![]() 1
1
=﹣ ![]() (m+3)2+
(m+3)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴m=﹣3時,△PBD的面積最大,此時P(﹣3, ![]()
如圖2中,作Q關于y軸的對稱點Q′,將Q′向左平移 ![]() 個單位得到Q″,連接PQ″交拋物線對稱軸于M,此時PM+MN+NQ最短.
個單位得到Q″,連接PQ″交拋物線對稱軸于M,此時PM+MN+NQ最短.
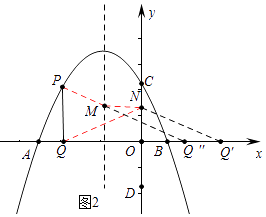
易證四邊形MNQ′Q″是平行四邊形,
∴NQ=NQ′=Q″M,
∴PM+MN+NQ=PM+MQ″+MN=PQ″+MN,
∵Q″( ![]() ,0),
,0),
∴PQ″= ![]() =
= ![]() ,
,
∴PM+MN+NQ的最小值為 ![]() +
+ ![]()
(3)解:如圖3中,
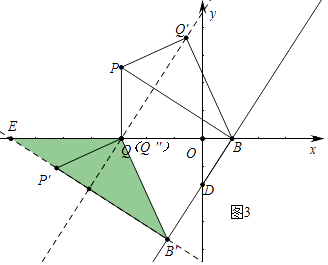
由(2)可知直線PB的解析式為y=﹣ ![]() x+
x+ ![]() ,直線BD的解析式為y=
,直線BD的解析式為y= ![]() x﹣
x﹣ ![]() ,
,
易證∠PBQ=30°,∠DBO=60°,PB⊥BD.
①當點Q″與Q重合時,∵∠B′EQ=∠QB′E=30°,
∴EQ=B′Q″=4,
∴OE=QE+OQ=7.
②如圖4中,當B′E=B′Q″時作B′N⊥x軸于N.

∵B′E=B′Q″=4,∠B′EN=30°,
∴B′N= ![]() B′E=2,EN=2
B′E=2,EN=2 ![]() ,
,
∴B′( ![]() ,﹣2),
,﹣2),
∴OE=2 ![]() +
+ ![]() =
= ![]() ﹣1.
﹣1.
③如圖5中,當EQ″=EB′時,作B′N⊥x軸于N.
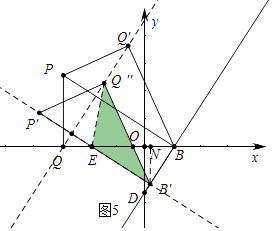
易知EP′=EQ″=EB′= ![]() ,B′N=
,B′N= ![]() ,EN=2,
,EN=2,
∴B′( ![]() ,﹣
,﹣ ![]() ),
),
∴EO= ![]() .
.
④如圖6中,當B′E=B′Q″時,
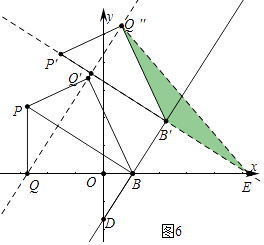
易知B′E=B′Q″=4,
在Rt△BEB′中,BE=EB′÷cos30°= ![]() ,
,
∴OE=OB+BE= ![]() +1,
+1,
綜上所述,滿足條件的OE的值為7或 ![]() ﹣1或
﹣1或 ![]() 或
或 ![]() +1.
+1.
【解析】(2)利用函數思想解決最值問題,設出未知數,把△PDB分割成S△PDB=S△PDK+S△PBK﹣S△DKB,用m的代數式分別表示出三個三角形的面積,構建出函數,配成頂點時,求出最值;幾條線段的和PM+MN+NQ最小值問題可利用對稱法,把線段和轉化為一條直線上的線段即可;(3)等腰三角形的分類,可就哪兩條邊是腰分類:B′E=B′Q;或點Q″與Q重合;或B′E=B′Q″或EQ″=EB′或B′E=B′Q″即可求出OE的長.


 寒假大串聯(lián)黃山書社系列答案
寒假大串聯(lián)黃山書社系列答案科目:初中數學 來源: 題型:
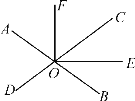
【題目】如圖,直線AB,CD相交于點O,OE是∠COB的平分線,∠FOE=90°,若∠AOD=70°.
(1)求∠BOE的度數;
(2)OF是∠AOC的平分線嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在正方形ABCD中,F(xiàn)是CD邊上一點(不和C,D重合),過點D做DG⊥BF交BF延長線于點G.連接AG,交BD于點E,連接EF,交CD于點M.若DG=6,AG=7 ![]() ,則EF的長為 .
,則EF的長為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數y=ax+b(a≠0)的圖象與反比例函數y= ![]() (k≠0)的圖象相交于A,B兩點,與y軸交于點C,與x軸交于點D,點D的坐標為(﹣1,0),點A的橫坐標是1,tan∠CDO=2.過點B作BH⊥y軸交y軸于H,連接AH.
(k≠0)的圖象相交于A,B兩點,與y軸交于點C,與x軸交于點D,點D的坐標為(﹣1,0),點A的橫坐標是1,tan∠CDO=2.過點B作BH⊥y軸交y軸于H,連接AH.
(1)求一次函數和反比例函數的解析式;
(2)求△ABH面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為傳播奧運知識,小剛就本班學生對奧運知識的了解程度進行了一次調查統(tǒng)計:A:熟悉,B:了解較多,C:一般了解.圖1和圖2是他采集數據后,繪制的兩幅不完整的統(tǒng)計圖,請你根據圖中提供的信息解答以下問題:
(1)求該班共有多少名學生;
(2)在條形圖中,將表示“一般了解”的部分補充完整;
(3)在扇形統(tǒng)計圖中,計算出“了解較多”部分所對應的圓心角的度數;
(4)如果全年級共1000名同學,請你估算全年級對奧運知識“了解較多”的學生人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小文同學統(tǒng)計了他所在小區(qū)居民每天微信閱讀的時間,并繪制了直方圖.有以下說法:①小文同學一共統(tǒng)計了60人;②每天微信閱讀不足20分鐘的人數有8人;③每天微信閱讀30~40分鐘的人數最多;④每天微信閱讀0-10分鐘的人數最少.根據圖中信息,上述說法中正確的是( )

A. ①②③④ B. ①②③ C. ②③④ D. ③④
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com