Question

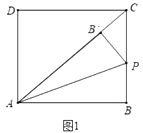
【題目】如圖1，在矩形中，，，動點從出發(fā)，以每秒1個單位的速度沿射線方向移動，作關(guān)于直線的對稱，設(shè)點的運動時間為．

（1）當(dāng)時．

①如圖2．當(dāng)點落在上時，顯然是直角三角形，求此時的值；

②當(dāng)點不落在上時，請直接寫出是直角三角形時的值；

（2）若直線與直線相交于點，且當(dāng)時，．問：當(dāng)，的大小是否發(fā)生變化，若不變，請說明理由．

Answer 1

【答案】（1）①，②或或；（2）不變，見解析

【解析】

（1）①利用勾股定理求出AC，再根據(jù)折疊的性質(zhì)以及勾股定理即可得出答案；②分三種情況進(jìn)行討論：①如圖2-1中，當(dāng)時，②如圖2-2中，當(dāng)時，③如圖2-3中，當(dāng)時，在中分別找出每條邊的長度，再利用勾股定理建立方程求解即可得出答案；

（2）首先證明ABCD是正方形，再利用全等三角形的性質(zhì)以及折疊的性質(zhì)即可得出答案．

解：（1）①如圖1中，∵四邊形是矩形，

∴，∴

∵翻折

∴，，

∴，

∴在中，

∴

∴；

②如圖2-1中，當(dāng)，在上時，

∵四邊形是矩形，∴，，，

∴

∴

在中，∵，

∴，

∴．

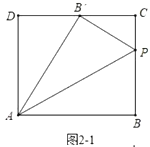
如圖2-2中，當(dāng)，在的延長線上時，

在中，，

∴

在中，則有：，

解得．

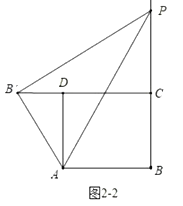
如圖2-3中，當(dāng)時，

易證四邊形為正方形，則．

綜上所述，滿足條件的的值為或或；

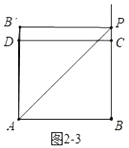
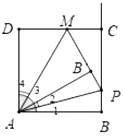
（2）當(dāng)時，如圖，∵

∴，

∵翻折，

∴，，

又∵，

∴，

∴，即四邊形是正方形，

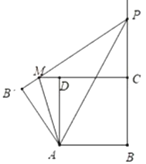
當(dāng)時，如圖，設(shè)

∴，

∴，

易證，

∴，

∵翻折，

∴，

∴，

∴，

∴．