
【題目】如圖,AB是⊙O的直徑,BC是⊙O的切線(xiàn),切點(diǎn)為B,OC相交于點(diǎn)D,且CD=2,BC=4,
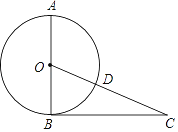
(1)求⊙O的半徑;
(2)連接AD并延長(zhǎng),交BC于點(diǎn)E,取BE的中點(diǎn)F,連接DF,試判斷DF與⊙O的位置關(guān)系,并說(shuō)明理由.
【答案】(1)3;(2)DF與⊙O相切;理由見(jiàn)解析;
【解析】
(1)設(shè)⊙O的半徑為R,由切線(xiàn)的性質(zhì)得出∠OBC=90°,由勾股定理得出方程,解方程即可;
(2)連接BD,由等腰三角形的性質(zhì)得出∠OBD=∠ODB,由圓周角定理得出∠ADB=90°,求出∠BDE=90°,由直角三角形的性質(zhì)得出DF=![]() BE=BF,得出∠DBF=∠BDF,證出∠BDF+∠ODB=90°,即可得出結(jié)論.
BE=BF,得出∠DBF=∠BDF,證出∠BDF+∠ODB=90°,即可得出結(jié)論.
(1)設(shè)⊙O的半徑為R,
∵BC是⊙O的切線(xiàn),
∴∠OBC=90°,
∴OB2+BC2=OC2 ,
即R2+42=(R+2)2 ,
解得:R=3,
即⊙O的半徑為3
(2)DF與⊙O相切;理由如下: 如圖所示:連接BD,
∵OB=OD,
∴∠OBD=∠ODB,
∵AB是⊙O的直徑,
∴∠ADB=90°,
∴∠BDE=90°,
∵F是BE的中點(diǎn),
∴DF=![]() BE=BF,
BE=BF,
∴∠DBF=∠BDF,
∵∠DBF+∠OBD=90°,
∴∠BDF+∠ODB=90°,
∴DF⊥OD,
∴DF與⊙O相切.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某工廠計(jì)劃生產(chǎn)甲、乙兩種產(chǎn)品共2500噸,每生產(chǎn)1噸甲產(chǎn)品可獲得利潤(rùn)0.3萬(wàn)元,每生產(chǎn)1噸乙產(chǎn)品可獲得利潤(rùn)0.4萬(wàn)元.設(shè)該工廠生產(chǎn)了甲產(chǎn)品x(噸),生產(chǎn)甲、乙兩種產(chǎn)品獲得的總利潤(rùn)為y(萬(wàn)元).
(1)求y與x之間的函數(shù)表達(dá)式;
(2)若每生產(chǎn)1噸甲產(chǎn)品需要A原料0.25噸,每生產(chǎn)1噸乙產(chǎn)品需要A原料0.5噸.受市場(chǎng)影響,該廠能獲得的A原料至多為1000噸,其它原料充足.求出該工廠生產(chǎn)甲、乙兩種產(chǎn)品各為多少?lài)崟r(shí),能獲得最大利潤(rùn).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
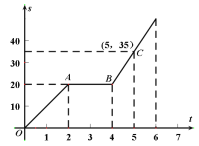
【題目】小明騎自行車(chē)從甲地到乙地,圖中的折線(xiàn)表示小明行駛的路程![]() 與所用時(shí)間
與所用時(shí)間![]() 之間的函數(shù)關(guān)系.試根據(jù)函數(shù)圖像解答下列問(wèn)題:
之間的函數(shù)關(guān)系.試根據(jù)函數(shù)圖像解答下列問(wèn)題:
(1)小明在途中停留了____![]() ,小明在停留之前的速度為____
,小明在停留之前的速度為____![]() ;
;
(2)求線(xiàn)段![]() 的函數(shù)表達(dá)式;
的函數(shù)表達(dá)式;
(3)小明出發(fā)1小時(shí)后,小華也從甲地沿相同路徑勻速向乙地騎行,![]()
![]() 時(shí),兩人同時(shí)到達(dá)乙地,求
時(shí),兩人同時(shí)到達(dá)乙地,求![]() 為何值時(shí),兩人在途中相遇.
為何值時(shí),兩人在途中相遇.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
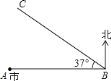
【題目】某日上午![]() 點(diǎn)鐘,
點(diǎn)鐘,![]() 市氣象局測(cè)得在城市正東方向
市氣象局測(cè)得在城市正東方向![]() 處
處![]() 點(diǎn)有一臺(tái)風(fēng)中心正在以
點(diǎn)有一臺(tái)風(fēng)中心正在以![]() 千米/時(shí)的速度沿西偏北
千米/時(shí)的速度沿西偏北![]() 的
的![]() 方向迅速移動(dòng)(如圖所示).據(jù)資料表明,在距離臺(tái)風(fēng)中心
方向迅速移動(dòng)(如圖所示).據(jù)資料表明,在距離臺(tái)風(fēng)中心![]() 范圍內(nèi)為嚴(yán)重影響區(qū)域(假定臺(tái)風(fēng)中心移動(dòng)方向不變,影響力不變).(參考數(shù)據(jù):
范圍內(nèi)為嚴(yán)重影響區(qū)域(假定臺(tái)風(fēng)中心移動(dòng)方向不變,影響力不變).(參考數(shù)據(jù):![]() ,
,![]() ).
).
(1)![]() 市會(huì)不會(huì)受這次臺(tái)風(fēng)的嚴(yán)重影響,為什么;
市會(huì)不會(huì)受這次臺(tái)風(fēng)的嚴(yán)重影響,為什么;
(2)如果![]() 市會(huì)受?chē)?yán)重影響,那么這次臺(tái)風(fēng)對(duì)
市會(huì)受?chē)?yán)重影響,那么這次臺(tái)風(fēng)對(duì)![]() 市嚴(yán)重影響多長(zhǎng)時(shí)間?
市嚴(yán)重影響多長(zhǎng)時(shí)間?
(3)![]() 市規(guī)定臺(tái)風(fēng)嚴(yán)重影響前一小時(shí)向市民發(fā)出預(yù)警警報(bào).如果
市規(guī)定臺(tái)風(fēng)嚴(yán)重影響前一小時(shí)向市民發(fā)出預(yù)警警報(bào).如果![]() 市會(huì)受這次臺(tái)風(fēng)嚴(yán)重影響,那么
市會(huì)受這次臺(tái)風(fēng)嚴(yán)重影響,那么![]() 市應(yīng)在幾點(diǎn)鐘發(fā)出預(yù)警警報(bào)?
市應(yīng)在幾點(diǎn)鐘發(fā)出預(yù)警警報(bào)?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,BD為△ABC的角平分線(xiàn),且BD=BC,E為BD延長(zhǎng)線(xiàn)上的一點(diǎn),BE=BA,過(guò)E作EF⊥AB,F為垂足,下列結(jié)論:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正確的是________(填序號(hào))

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
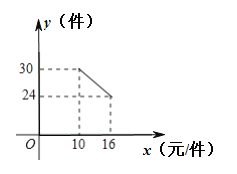
【題目】一名在校大學(xué)生利用“互聯(lián)網(wǎng)+”自主創(chuàng)業(yè),銷(xiāo)售一種產(chǎn)品,這種產(chǎn)品成本價(jià)10元/件,已知銷(xiāo)售價(jià)不低于成本價(jià),且物價(jià)部門(mén)規(guī)定這種產(chǎn)品的銷(xiāo)售價(jià)不高于16元/件,市場(chǎng)調(diào)查發(fā)現(xiàn),該產(chǎn)品每天的銷(xiāo)售量y(件)與銷(xiāo)售價(jià)x(元/件)之間的函數(shù)關(guān)系如圖所示.
(1)求y與x之間的函數(shù)關(guān)系式,并寫(xiě)出自變量x的取值范圍;
(2)求每天的銷(xiāo)售利潤(rùn)W(元)與銷(xiāo)售價(jià)x(元/件)之間的函數(shù)關(guān)系式,并求出每件銷(xiāo)售價(jià)為多少元時(shí),每天的銷(xiāo)售利潤(rùn)最大?最大利潤(rùn)是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
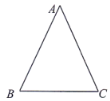
【題目】求證:等腰三角形兩腰上的中線(xiàn)相等.
(1)請(qǐng)用尺規(guī)作出△ABC兩腰上的中線(xiàn)BD、CE(保留痕跡,不寫(xiě)作法);
(2)結(jié)合圖形,寫(xiě)出已知、求證和證明過(guò)程.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
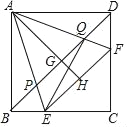
【題目】如圖,正方形ABCD的邊長(zhǎng)為10,點(diǎn)E、F分別在邊BC、CD上,且∠EAF=45°,AH⊥EF于點(diǎn)H,AH=10,連接BD,分別交AE、AH、AF于點(diǎn)P、G、Q.
(1)求△CEF的周長(zhǎng);
(2)若E是BC的中點(diǎn),求證:CF=2DF;
(3)連接QE,求證:AQ=EQ.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
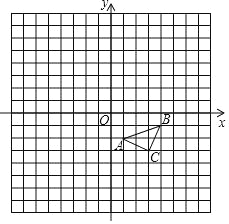
【題目】如圖.在平面直角坐標(biāo)系內(nèi),△ABC三個(gè)頂點(diǎn)的坐標(biāo)分別為A(1,﹣2),B(4,﹣1),C(3,﹣3)(正方形網(wǎng)格中,每個(gè)小正方形的邊長(zhǎng)都是1個(gè)單位長(zhǎng)度).
(1)作出△ABC向左平移5個(gè)單位長(zhǎng)度,再向下平移3個(gè)單位長(zhǎng)度得到的△A1B1C1;
(2)以坐標(biāo)原點(diǎn)O為位似中心,相似比為2,在第二象限內(nèi)將△ABC放大,放大后得到△A2B2C2作出△A2B2C2;
(3)以坐標(biāo)原點(diǎn)O為旋轉(zhuǎn)中心,將△ABC逆時(shí)針旋轉(zhuǎn)90°,得到△A3B3C3,作出△A3B3C3,并求線(xiàn)段AC掃過(guò)的面積.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com