
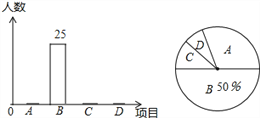
【題目】某校的20年校慶舉辦了四個項目的比賽,現分別以A,B,C,D表示它們.要求每位同學必須參加且限報一項.以701班為樣本進行統計,并將統計結果繪制如下兩幅統計圖,其中參加A項目的人數比參加C與D項目人數的總和多1人,參加D項目的人數比參加A項目的人數少11人.請你結合圖中所給出的信息解答下列問題:
(1)求出全班總人數;
(2)求出扇形統計圖中參加D項目比賽的學生所在的扇形圓心角的度數;
(3)若該校7年級學生共有200人,請你估計這次活動中參加A和B項目的學生共有多少人?
【答案】(1)總數為:50;
(2)參加D項目的學生所占扇形圓心角為14.4°;
(3)參加A、B項目的學生人數:152人.
【解析】試題分析:(1)根據B項的人數為25占50%,所以2乘25即總數,(2)根據題意,設參加D項目的人數為x人,C項目的人數為y人,列出方程組,求出D項目人數,再用D項目人數除以總數再360°,即為參加D項目的學生所占扇形圓心角度數.(3)根據參加A、B項目的學生人數=7年級學生總數×A、B項目的學生人數百分比.
試題解析:(1)總數為:2×25=50;
(2)設參加D項目的人數為x人,C項目的人數為y人,則A項目的人數為(x+11)人.
依題意得: ![]()
解得: ![]() ,
,
所以參加D項目人數:2人;
參加D項目的學生所占扇形圓心角: ![]() ×360°=14.4°;
×360°=14.4°;
(3)參加A、B項目的學生人數: ![]() =152(人).
=152(人).


 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:初中數學 來源: 題型:
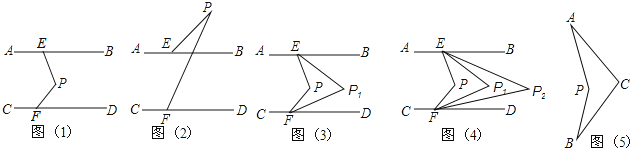
【題目】如圖(1),直線AB∥CD,點P在兩平行線之間,點E在AB上,點F在CD上,連結PE,PF.
(1)∠PEB,∠PFD,∠EPF滿足的數量關系是 ,并說明理由.
(2)如圖(2),若點P在直線AB上側時,∠PEB,∠PFD,∠EPF滿足的數量關系是 (不需說明理由)
(3)如圖(3),在圖(1)基礎上,P![]() E平分∠PEB,P
E平分∠PEB,P![]() F平分∠PFD,若設∠PEB=x°,∠PFD=y°.則∠P
F平分∠PFD,若設∠PEB=x°,∠PFD=y°.則∠P![]() =______(用x,y的代數式表示),若P
=______(用x,y的代數式表示),若P![]() E平分∠P
E平分∠P![]() EB,P
EB,P![]() F平分∠P
F平分∠P![]() FD,可得∠P
FD,可得∠P![]() ,P
,P![]() E平分∠P
E平分∠P![]() EB,P
EB,P![]() F平分∠P
F平分∠P![]() FD,可得∠P
FD,可得∠P![]() …,依次平分下去,則∠P
…,依次平分下去,則∠P![]() =______.
=______.
(4)科技活動課上,雨軒同學制作了一個圖(5)的“飛旋鏢”,經測量發現∠PAC=28°,
∠PBC=30°,他很想知道∠APB與∠ACB的數量關系,你能告訴他嗎?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BD是∠ABC平分線,DE![]() AB于E,AB=36cm,BC=24cm,S△ABC =144cm2,則DE的長是( )
AB于E,AB=36cm,BC=24cm,S△ABC =144cm2,則DE的長是( )

A. 4.8cm B. 4.5cm C. 4 cm D. 2.4cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【問題情境】一節數學課后,老師布置了一道課后練習題:
如圖:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于點D,點E、F分別在A和BC上,∠1=∠2,FG⊥AB于點G,求證:△CDE≌△EGF.
(1)閱讀理解,完成解答
本題證明的思路可用下列框圖表示: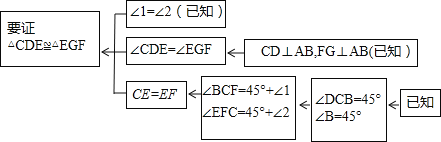
根據上述思路,請你完整地書寫這道練習題的證明過程;
(2)特殊位置,證明結論
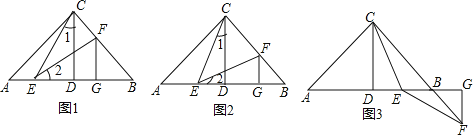
若CE平分∠ACD,其余條件不變,求證:AE=BF;
(3)知識遷移,探究發現
如圖,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于點D,若點E是DB的中點,點F在直線CB上且滿足EC=EF,請直接寫出AE與BF的數量關系.(不必寫解答過程)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com