
問題:如圖1,在正方形ABCD內有一點P,PA=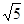 ,PB=
,PB=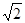 ,PC=1,求∠BPC的角度.
,PC=1,求∠BPC的角度.
分析:根據已知條件比較分散的特點,我們可以通過旋轉變換,將分散的已知條件集中在一起,于是將△BPC繞點B逆時針旋轉900,得到了△BP1A(如圖2),然后連接PP1.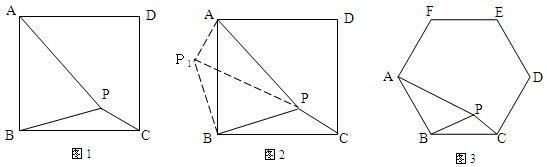
解決問題:請你通過計算求出圖2中∠BPC的角度;
類比研究:如圖3,若在正六邊形ABCDEF內有一點P,且PA=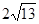 ,PB=4,PC=2.
,PB=4,PC=2.
(1)請你通過計算求出∠BPC的度數;
(2)直接寫出正六邊形ABCDEF的邊長為 .
解決問題1350;類比研究(1)1200;(2)2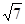
解析試題分析:(1)根據旋轉的性質得到∠P′BP=90°,BP′=BP=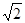 ,P′A=PC=1,∠BP′A=∠BPC,則△BPP′為等腰直角三角形,根據等腰直角三角形的性質得PP′=
,P′A=PC=1,∠BP′A=∠BPC,則△BPP′為等腰直角三角形,根據等腰直角三角形的性質得PP′=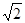 PB=2,∠BP′P=45°,利用勾股定理的逆定理可得到△APP′為直角三角形,且∠AP′P=90°,則∠BPC=∠BP′A=45°+90°=135°;
PB=2,∠BP′P=45°,利用勾股定理的逆定理可得到△APP′為直角三角形,且∠AP′P=90°,則∠BPC=∠BP′A=45°+90°=135°;
(2)把△BPC繞點B逆時針旋轉120°,得到了△BP′A,根據旋轉的性質得到∠P′BP=120°,BP′=BP=4,P′A=PC=2,∠BP′A=∠BPC,則∠BP′P=∠BPP′=30°,得到P′H=PH,利用含30°的直角三角形三邊的關系得到BH=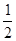 BP′=2,P′H=
BP′=2,P′H= BH=2
BH=2 ,得到P′P=2P′H=4
,得到P′P=2P′H=4 ,再利用勾股定理的逆定理可得到△APP′為直角三角形,且∠AP′P=90°,于是有∠BPC=∠BP′A=30°+90°=120°;過A作AG⊥BP′于G點,利用含30°的直角三角形三邊的關系得到GP′=
,再利用勾股定理的逆定理可得到△APP′為直角三角形,且∠AP′P=90°,于是有∠BPC=∠BP′A=30°+90°=120°;過A作AG⊥BP′于G點,利用含30°的直角三角形三邊的關系得到GP′=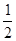 AP′=1,AG=
AP′=1,AG= GP′=
GP′= ,然后在Rt△AGB中利用勾股定理即可計算出AB長.
,然后在Rt△AGB中利用勾股定理即可計算出AB長.
(1)∵△BPC繞點B逆時針旋轉90°,得到了△BP′A,
∴∠P′BP=90°,BP′=BP=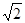 ,P′A=PC=1,∠BP′A=∠BPC,
,P′A=PC=1,∠BP′A=∠BPC,
∴△BPP′為等腰直角三角形,
∴PP′=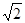 PB=2,∠BP′P=45°,
PB=2,∠BP′P=45°,
在△APP′中,AP=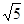 ,PP′=2,AP′=1,
,PP′=2,AP′=1,
∵(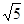 )2=22+12,
)2=22+12,
∴AP2=PP′2+AP′2,
∴△APP′為直角三角形,且∠AP′P=90°
∴∠BP′A=45°+90°=135°,
∴∠BPC=∠BP′A=135°;
(2)∵六邊形ABCDEF為正六邊形,
∴∠ABC=120°,
把△BPC繞點B逆時針旋轉120°,得到了△BP′A,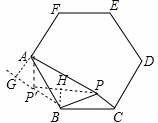
∴∠P′BP=120°,BP′=BP=4,P′A=PC=2,∠BP′A=∠BPC,
∴∠BP′P=∠BPP′=30°,
過B作BH⊥PP′于H,
∵BP′=BP,
∴P′H=PH,
在Rt△BP′H中,∠BP′H=30°,BP′=4,
∴BH=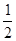 BP′=2,P′H=
BP′=2,P′H= BH=2
BH=2 ,
,
∴P′P=2P′H=4 ,
,
在△APP′中,AP=2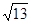 ,PP′=4
,PP′=4 ,AP′=2,
,AP′=2,
∵(2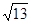 )2=(4
)2=(4 )2+22,
)2+22,
∴AP2=PP′2+AP′2,
∴△APP′為直角三角形,且∠AP′P=90°,
∴∠BP′A=30°+90°=120°,
∴∠BPC=120°,
過A作AG⊥BP′于G點,
∴∠AP′G=60°,
在Rt△AGP′中,AP′=2,∠GAP′=30°,
∴GP′=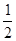 AP′=1,AG=
AP′=1,AG= GP′=
GP′= ,
,
在Rt△AGB中,GB=GP′+P′B=1+4=5,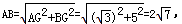
即正六邊形ABCDEF的邊長為2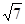 .
.
考點:旋轉的性質,正方形的性質、等腰直角三角形的判定與性質、勾股定理與逆定理,含30°的直角三角形的性質
點評:解題的關鍵是熟記旋轉的性質:旋轉前后兩圖形全等,即對應角相等,對應線段相等;對應點與旋轉中心的連線段的夾角等于旋轉角.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
| 行駛方向 | 速度的大小(km/h) | 出發前的位置 | |
| 甲車 | |||
| 乙車 |
查看答案和解析>>
科目:初中數學 來源: 題型:



查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:學習周報 數學 華師大八年級版 2009-2010學年 第13期 總第169期 華師大版 題型:044
工具閱讀:
在平面上畫兩條原點重合、互相垂直且具有相同單位長度的數軸(如圖),這就建立了平面直角坐標系.通常把其中水平的一條數軸叫做x軸或橫軸,取向右為正方向;鉛直的數軸叫做y軸或縱軸,取向上為正方向;兩數軸的交點O叫做坐標原點.

問題探究:如圖1,在6×6的方格紙中,給出如下三種變換:P變換,Q變換,R變換.

將圖形F沿x軸向右平移1格得圖形F1,稱為作1次P變換;
將圖形F沿y軸翻折得圖形F2,稱為作1次Q變換;
將圖形F繞坐標原點順時針旋轉90°得圖形F3,稱為作1次R變換.
規定:PQ變換表示先作1次Q變換,再作1次P變換;QP變換表示先作1次P變換,再作1次Q變換;Rn變換表示作n次R變換.
解答下列問題:
(1)作R4變換相當于至少作________次Q變換;
(2)請在圖2中畫出圖形F作R2011變換后得到的圖形F4;

(3)PQ變換與QP變換是否是相同的變換?請在圖3中畫出PQ變換后得到的圖形F5,在圖4中畫出QP變換后得到的圖形F6.

查看答案和解析>>
科目:初中數學 來源:同步題 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com