
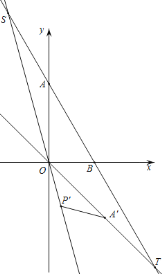
【題目】如圖,在直角坐標系![]() 中,
中,![]() ,
,![]() ,
,![]() 是線段
是線段![]() 上靠近點
上靠近點![]() 的三等分點.
的三等分點.

(1)求點![]() 的坐標;
的坐標;
(2)若點![]() 是
是![]() 軸上的一動點,連接
軸上的一動點,連接![]() 、
、![]() ,當
,當![]() 的值最小時,求出
的值最小時,求出![]() 的坐標及
的坐標及![]() 的最小值;
的最小值;
(3)如圖2,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,再將
,再將![]() 繞點
繞點![]() 作順時針方向旋轉,旋轉角度為
作順時針方向旋轉,旋轉角度為![]() ,記旋轉中的三角形為
,記旋轉中的三角形為![]() ,在旋轉過程中,直線
,在旋轉過程中,直線![]() 與直線
與直線![]() 的交點為
的交點為![]() ,直線
,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,當
,當![]() 為等腰三角形時,請直接寫出
為等腰三角形時,請直接寫出![]() 的值.
的值.
【答案】(1)![]() ;(2)最小值
;(2)最小值![]() ,M
,M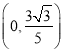 ;(3)
;(3)![]() 、
、![]() 、
、![]() 、
、![]()
【解析】
(1)過點![]() 作
作![]() 軸于點
軸于點![]() ,證得
,證得![]() ,然后由相似三角形的性質求得
,然后由相似三角形的性質求得![]() ,從而求得GB,HG的長度,使問題得解;
,從而求得GB,HG的長度,使問題得解;
(2)作點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() ,連接
,連接![]() 交
交![]() 軸于點
軸于點![]() ,此時
,此時![]() 的值最小即
的值最小即![]() 的長度,根據勾股定理求
的長度,根據勾股定理求![]() 長度,然后利用待定系數法求直線
長度,然后利用待定系數法求直線![]() 的函數解析式,從而求與y軸交點坐標,使問題得解;
的函數解析式,從而求與y軸交點坐標,使問題得解;
(3)依據△OST為等腰三角形,分4種情況畫出圖形,即可得到旋轉角的度數.
解:(1)如圖,過點![]() 作
作![]() 軸于點
軸于點![]() .
.
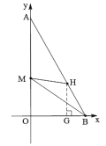
因為![]() 軸
軸
∴HG∥OA
∴![]() ,
,
又∵![]() 是線段
是線段![]() 上靠近點
上靠近點![]() 的三等分點
的三等分點
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴![]()
∴![]()
(2)如圖,作點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() ,連接
,連接![]() 交
交![]() 軸于點
軸于點![]() .
.
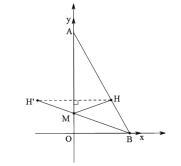
則![]() 為
為![]() ,
, ![]()
此時![]()
∴![]() 的最小值為
的最小值為![]() ;
;
設直線![]() :
:![]() ,把
,把![]()
![]() ,B(3,0)代入得:
,B(3,0)代入得:
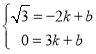 ,解得:
,解得: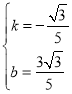
∴直線![]() 為
為![]()
當![]() 時,
時,![]()
∴![]() 為
為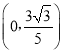
(3)如圖,當OT=OS時,α=75°-30°=45°;
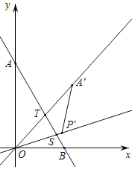
如圖,當OT=TS時,α=90°;
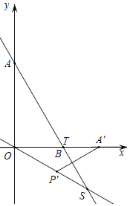
如圖,當OT=OS時,α=90°+60°-15°=135°;
如圖,當ST=OS時,α=180°;
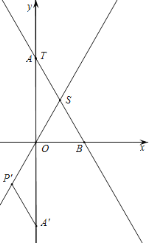
綜上所述,α的值為45°,90°,135°,180°.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于點D,PE⊥OB于點E.如果點M是OP的中點,則DM的長是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC中,M是邊BC延長線上一點,連接AM交△ABC的外接圓于點D,延長BD至N,使得BN=AM,連接CN、MN,
(1)求證:△CMN是等邊三角形;
(2)判斷CN與⊙O的位置關系,并說明理由;
(3)若AD:AB=3:4,BN=4,求等邊△ABC的邊長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市教育行政部門為了了解初一學生每學期參加綜合實踐活動的情況,隨機抽樣調查了某校初一學生一個學期參加綜合實踐活動的天數,并用得到的數據繪制了下面兩幅不完整的統計圖,請你根據圖中提供的信息,回答下列問題:

(1)扇形統計圖中a的值為_____,“活動時間為4天”的扇形所對圓心角的度數為_____°,該校初一學生的總人數為______;
(2)補全頻數分布直方圖;
(3)如果該市共有初一學生6000人,請你估計“活動時間不少于4天”的大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
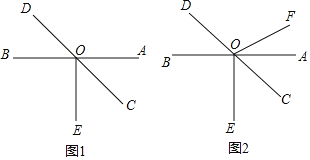
【題目】如圖,AB、CD交于點O,OE⊥AB,且OC平分∠AOE.
(1)如圖1,求∠BOD的度數;
(2)如圖2,過O點作射線OF,且∠DOF=4∠AOF,求∠FOC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題6分)甲、乙兩人進行摸牌游戲.現有三張形狀大小完全相同的牌,正面分別標有數字2,3,5.將三張牌背面朝上,洗勻后放在桌子上.
(1)甲從中隨機抽取一張牌,記錄數字后放回洗勻,乙再隨機抽取一張.請用列表法或畫樹狀圖的方法,求兩人抽取相同數字的概率;
(2)若兩人抽取的數字和為2的倍數,則甲獲勝;若抽取的數字和為5的倍數,則乙獲勝.這個游戲公平嗎?請用概率的知識加以解釋.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題8分)如圖某幢大樓頂部有廣告牌CD.張老師目高MA為1.60米,他站立在離大樓45米的A處測得大樓頂端點D的仰角為30°;接著他向大樓前進14米、站在點B處,測得廣告牌頂端點C的仰角為45°.(取![]() ,計算結果保留一位小數)
,計算結果保留一位小數)

(1)求這幢大樓的高DH;
(2)求這塊廣告牌CD的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為a, P為正方形邊上一動點,運動路線是A-D-C-B-A,設P點經 過的路程為x,以點A,P,D為頂點的三角形的面積是y,圖象反映了y與x的關系,當![]() 時,x=_____.
時,x=_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com