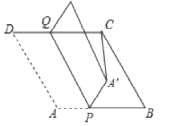
【題目】如圖,在菱形ABCD中,AB=8,∠B=60°,P是AB上一點,BP=5,Q是CD邊上ー動點,將四邊形APQD沿直線PQ折疊,A的對應點A`.當CA`的長度最小時,則CQ的長為( )
A. 7B. 2
C. 2
D. 4
【答案】A
【解析】
由A`P=3可知點A`在以P為圓心以PA`為半徑的弧上,故此當C,P,A`在一條直線上時,CA`有最小值,過點C作CH⊥AB,垂足為H,先求得BH、HC的長,則可得到PH的長,然后再求得PC的長,最后依據折疊的性質和平行線的性質可證明△CQP為等腰三角形,則可得到Q℃的長
如圖所示:過點C作CH⊥AB,垂足為H
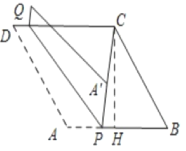
在Rt△BCH中,∠B=60°,BC=8,則
BH=
BC=4,CH=sin60°BC=
8=4
.
∴PH=1
在Rt△CPH中,依據勾股定理可知
PC=
由翻折的性質可知:∠APQ=∠A'PQ
∵DC∥AB
∴∠CQP=∠APQ
∴∠CQP=∠CPQ.
∴QC=CP=7.
故選:A
科目：初中數學 來源： 題型：
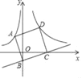
【題目】如圖，直線y＝mx﹣1交y軸于點B，交x軸于點C，以BC為邊的正方形ABCD的頂點A（﹣1，a）在雙曲線y＝﹣
（x＜0）上，D點在雙曲線y＝
（x＞0）上，則k的值為（ ）
A. 6 B. 5 C. 3 D. 2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠ABD＝∠ABC，補充一個條件，使得△ABD≌△ABC，則下列選項不符合題意的是（ ）
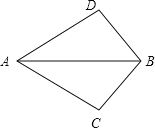
A. ∠D＝∠CB. ∠DAB＝∠CABC. BD＝BCD. AD＝AC
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，∠AOB＝70°，以點O為圓心，以適當長為半徑作弧分別交OA，OB于C，D兩點；分別以C，D為圓心，以大于
CD的長為半徑作弧，兩弧相交于點P；以O為端點作射線OP，在射線OP上取點M，連接MC、MD．若測得∠CMD＝40°，則∠MDB＝_____
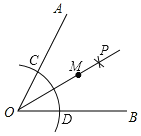
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了慶祝“五四”青年節，我市某中學舉行了書法比賽，賽后隨機抽查部分參賽同學成績（滿分為100分），并制作成圖表如下
分數段 | 頻數 | 頻率 |
60≤x＜70 | 30 | 0.15 |
70≤x＜80 | m | 0.45 |
80≤x＜90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
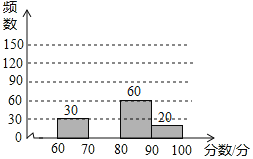
請根據以上圖表提供的信息，解答下列問題：
（1）這次隨機抽查了 名學生；表中的數m＝ ，n＝ ；
（2）請在圖中補全頻數分布直方圖；
（3）若繪制扇形統計圖，分數段60≤x＜70所對應扇形的圓心角的度數是 ；
（4）全校共有600名學生參加比賽，估計該校成績不低于80分的學生有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，為了測量山坡上旗桿CD的高度，小明在點A處利用測角儀測得旗桿頂端D的仰角為37°，然后他沿著正對旗桿CD的方向前進17m到達B點處，此時測得旗桿頂部D和底端C的仰角分別為58°和30°，求旗桿CD的高度（結果精確到0.1m）．
（參考數據：sin58°≈0.85，cos58°≈0.53，tan58°≈1.6，sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，
≈1.73）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】解不等式組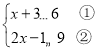
.請結合題意填空，完成本題的解答
（Ⅰ）解不等式①，得__________；
（Ⅱ）解不等式②，得__________；
（Ⅲ）把不等式①和②的解集在數軸上表示出來：
（Ⅳ）原不等式組的解集為__________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】關于x的一元二次方程x2﹣(2k﹣1)x+k2+1＝0有兩個不相等的實數根x1，x2．
(1)求實數k的取值范圍；
(2)若方程的兩實數根x1，x2滿足|x1|+|x2|＝x1x2，求k的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AD平分∠BAC,按如下步驟作圖：第一步，分別以點A、D為圓心，以大于
的長為半徑在AD的兩側作弧，交于兩點M、N;第二步，連結MN，分別交AB、AC于點E、F；第三步，連結DE、DF．．若BD=6，AF=4，CD=3，則BE的長是（ ）
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com