
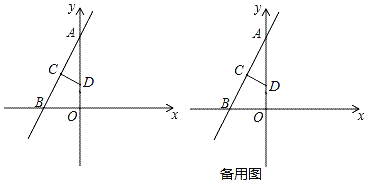
【題目】如圖,在平面直角坐標系中,A(0,8),B(﹣4,0),線段AB的垂直平分線CD分別交AB、OA于點C、D,其中點D的坐標為(0,3).
(1)求直線AB的解析式;
(2)求線段CD的長;
(3)點E為y軸上一個動點,當△CDE為等腰三角形時,求E點的坐標.
【答案】(1)直線AB的解析式為y=2x+8;(2)CD=![]() ;(3)滿足題意的點E坐標為(0,5+
;(3)滿足題意的點E坐標為(0,5+![]() )或(0,5﹣
)或(0,5﹣![]() )或(0,5)或(0,
)或(0,5)或(0,![]() ).
).
【解析】
(1)用待定系數法求解即可;
(2)先由勾股定理求出AB的長,再由垂直平分線的性質求出AC的長,然后證明△CAD∽△OAB,利用相似三角形的對應邊成比例即可求出CD的長,
(3)先由△CAD∽△OAB,求出AD和OD的長,然后分當CD=DE時,當CD=CE時,當CE=DE時三種情況求解即可;
(1)∵A(0,8),
∴設直線AB的解析式為y=kx+8,
∵B(﹣4,0),
∴﹣4k+8=0,
∴k=2,
∴直線AB的解析式為y=2x+8;
(2)∵A(0,8),B(﹣4,0),
∴OA=8,OB=4,AB=4![]() ,
,
∵CD是AB的垂直平分線,
∴∠ACD=90°,AC=![]() AB=2
AB=2![]() ,
,
∵∠ACD=∠AOB=90°,∠CAD=∠OAB,
∴△CAD∽△OAB,
∴![]() ,
,
∴![]() ,
,
∴CD=![]() ,
,
(3)∵△CAD∽△OAB,
∴![]() ,
,
∴![]() ,
,
∴AD=5,
∴OD=OA﹣AD=3,D(0,3),
當CD=DE時,DE=![]() ,
,
∴E(0,5+![]() )或(0,5﹣
)或(0,5﹣![]() ),
),
當CD=CE時,如圖1,
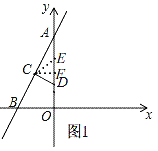
∵A(0,8),B(﹣4,0),
∴C(﹣2,4),
過點C作CF⊥y軸于F,
∴DF=EF,F(0,4),
∴E(0,5);
當CE=DE時,如圖2,過E作E'G⊥CD,則E'G是線段CD的中垂線,

∵AB⊥CD,
∴E'G是△ACD的中位線,
∴DE'=AE'=![]() AD=
AD=![]() ,
,
∴OE'=OD+DE'=![]() ,
,
∴E(0,![]() ),
),
即:滿足題意的點E坐標為(0,5+![]() )或(0,5﹣
)或(0,5﹣![]() )或(0,5)或(0,
)或(0,5)或(0,![]() ).
).


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,對角線AC,BD交于點O,已知∠AOD=120°,AC=16,則圖中長度為8的線段有( )

A. 2條 B. 4條 C. 5條 D. 6條
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過A(1,0)、B(3,0)作x軸的垂線,分別交直線y=4﹣x于C、D兩點.拋物線y=ax2+bx+c經過O、C、D三點.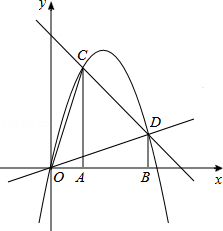
(1)求拋物線的表達式;
(2)點M為直線OD上的一個動點,過M作x軸的垂線交拋物線于點N,問是否存在這樣的點M,使得以A、C、M、N為頂點的四邊形為平行四邊形?若存在,求此時點M的橫坐標;若不存在,請說明理由;
(3)若△AOC沿CD方向平移(點C在線段CD上,且不與點D重合),在平移的過程中△AOC與△OBD重疊部分的面積記為S,試求S的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展校園足球運動,某縣城區四校決定聯合購買一批足球運動裝備,市場調查發現:甲、乙兩商場以同樣的價格出售同種品牌的足球隊服和足球,已知每套隊服比每個足球多50元,兩套隊服與三個足球的費用相等,經洽談,甲商場優惠方案是:每購買十套隊服,送一個足球;乙商場優惠方案是:若購買隊服超過80套,則購買足球打八折.
(1)求每套隊服和每個足球的價格是多少?
(2)若城區四校聯合購買100套隊服和a個足球,請用含a的式子分別表示出到甲商場和乙商場購買裝備所花的費用;
(3)假如你是本次購買任務的負責人,你認為到哪家商場購買比較合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,AC=BC,點D在邊AB上,連接CD,將線段CD繞點C順時針旋轉90°至CE位置,連接AE. 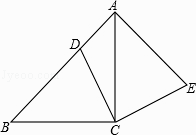
(1)求證:AB⊥AE;
(2)若BC2=ADAB,求證:四邊形ADCE為正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,現有一張邊長為4的正方形紙片ABCD,點P為正方形AD邊上的一點(不與點A、點D重合)將正方形紙片折疊,使點B落在P處,點C落在G處,PG交DC于H,折痕為EF,連接BP、BH. 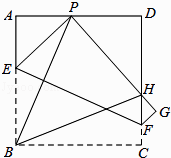
(1)求證:∠APB=∠BPH;
(2)當點P在邊AD上移動時,△PDH的周長是否發生變化?并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長都為 a 的正方形內分別排列著一些大小相等的圓:
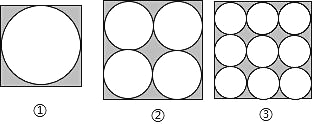
(1)根據圖中的規律,第 4 個正方形內圓的個數是 ,第n 個正方形內圓的個數是_____.
(2)如果把正方形內除去圓的部分都涂上陰影.
①用含a 的代數式分別表示第 1 個正方形中、第 3 個正方形中陰影部分的面積(結果保留π);
②若 a=10,請直接寫出第 2018 個正方形中陰影都分的面積 (結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果∠A和∠B互補,且∠A>∠B,給出下列四個式子:①90°﹣∠B;②∠A﹣90°;③![]() (∠A+∠B)④
(∠A+∠B)④![]() (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序號)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠A=120°,∠C=80°.將△BMN沿著MN翻折,得到△FMN.若MF∥AD,FN∥DC,則∠F的度數為( )
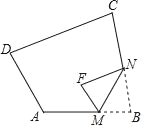
A. 70° B. 80° C. 90° D. 100°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com