
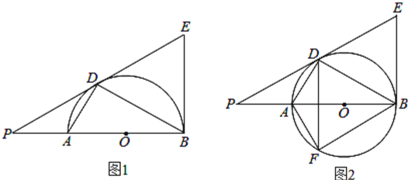
【題目】如圖,AB是圓O的直徑,O為圓心,AD、BD是半圓的弦,且∠PDA=∠PBD.延長PD交圓的切線BE于點E.
(1)證明:直線PD是⊙O的切線;
(2)如果∠BED=60°,PD=![]() ,求PA的長;
,求PA的長;
(3)將線段PD以直線AD為對稱軸作對稱線段DF,點F正好在圓O上,如圖2,求證:四邊形DFBE為菱形.
【答案】(1)見解析;(2)1;(3)見解析
【解析】
(1)連接OD,由AB是圓O的直徑可得∠ADB=90°,再利用角度的相互轉換求得∠ADO+∠PDA=90°,即可得出直線PD為⊙O的切線;
(2)求出∠P=30°,解直角三角形求出OD,結合勾股定理可得出PO,最后根據PA=PO-AO可得出結果;
(3)根據折疊和已知求出∠P=∠PBF,根據平行線的判定推出DE∥BF,求出DF⊥AB,BE⊥AB,推出DF∥BE,求出ED=EB,根據菱形的判定推出即可.
(1)證明:如圖1,連接OD,

∵AB是圓O的直徑,∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
又∵DO=BO,∴∠BDO=∠PBD,
∵∠PDA=∠PBD,∴∠BDO=∠PDA,
∴∠ADO+∠PDA=90°,即PD⊥OD,
∵點D在⊙O上,
∴直線PD為⊙O的切線.
(2)解:∵BE是⊙O的切線,∴∠EBA=90°,
∵∠BED=60°,∴∠P=30°,
∵PD為⊙O的切線,∴∠PDO=90°,
在Rt△PDO中,∠P=30°,PD=![]() ,
,
∴![]() ,解得OD=1,
,解得OD=1,
∴![]() ,
,
∴PA=PO﹣AO=2﹣1=1.
(3)證明:如圖2中,依題意得:∠ADF=∠PDA,∠APD=∠AFD,
∵∠PDA=∠PBD,∠ADF=∠ABF,∠AFD=∠PBD,
∴∠ADF=∠AFD=∠APD=∠ABF,
∴AD=AF,BF∥PD,即BF∥DE.
又∠DAB+∠DBA=90°,∴∠DAB+∠ADF=90°,
∴DF⊥PB.
∵BE為切線,
∴BE⊥PB,
∴DF∥BE,
∴四邊形DFBE為平行四邊形,
∵PE、BE為切線,
∴BE=DE,
∴四邊形DFBE為菱形.


科目:初中數學 來源: 題型:
【題目】某校七年級甲班、乙班舉行一分鐘投籃比賽,每班派10名學生參賽,在規定時間內進球數不少于8個為優秀學生.比賽數據的統計圖表如下(數據不完整):
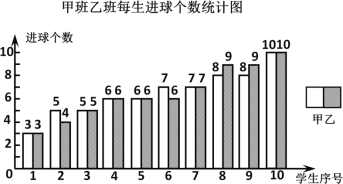

根據以上信息,解答下列問題:
(1)直接寫出a,b,c的值.
(2)你認為哪個班的比賽成績要好一些?請簡要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
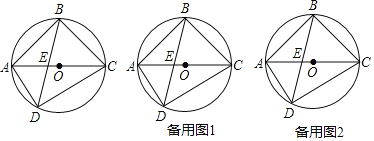
【題目】如圖,四邊形ABCD內接于⊙O,AC為直徑,AC和BD交于點E,AB=BC.
(1)求∠ADB的度數;
(2)過B作AD的平行線,交AC于F,試判斷線段EA,CF,EF之間滿足的等量關系,并說明理由;
(3)在(2)條件下過E,F分別作AB,BC的垂線,垂足分別為G,H,連接GH,交BO于M,若AG=3,S四邊形AGMO:S四邊形CHMO=8:9,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
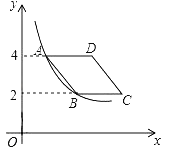
【題目】如圖,在平面直角坐標系中,菱形ABCD在第一象限內,邊BC與x軸平行,A,B兩點的縱坐標分別為4,2,反比例函數y=![]() (x>0)的圖象經過A,B兩點,若菱形ABCD的面積為2
(x>0)的圖象經過A,B兩點,若菱形ABCD的面積為2![]() ,則k的值為______.
,則k的值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角三角形ABC中,∠C=90°,AC=BC,E是AB的中點,過點E作AC和BC的垂線,垂足分別為點D和點F,四邊形CDEF沿著CA方向勻速運動,點C與點A重合時停止運動,設運動時間為t,運動過程中四邊形CDEF與△ABC的重疊部分面積為S.則S關于t的函數圖象大致為( )
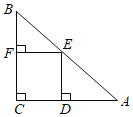
A. B.
B.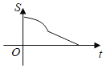 C.
C.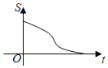 D.
D.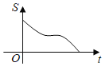
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】水果店購進某種水果的成本為10元/千克,經市場調研,獲得銷售單價p(元/千克)與銷售時間t(1≤t≤15,t為整數)(天)之間的部分數據如下表:
銷售時間t(1≤t≤15,t為整數)(天) | 1 | 4 | 5 | 8 | 12 |
銷售單價p(元/千克) | 20.25 | 21 | 21.25 | 22 | 23 |
已知p與t之間的變化規律符合一次函數關系.
(1)試求p關于t的函數表達式;
(2)若該水果的日銷量y(千克)與銷售時間t(天)的關系滿足一次函數y=-2t+120(1≤t≤15,t為整數).
① 求銷售過程中最大日銷售利潤為多少?
② 在實際銷售的前12天中,公司決定每銷售1千克水果就捐贈n元利潤(n<3)給“精準扶貧”對象.現發現:在前12天中,每天扣除捐贈后的日銷售利潤隨時間t的增大而增大,求n的取值范圍
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C是弧BE中點,AE⊥CD于點D,延長DC,AB交于點F,已知AD=4,FC=![]() FB.
FB.
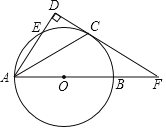
(1)求證:CD是⊙O的切線.
(2)求線段FC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在讀書月活動中,學校準備購買一批課外讀物.為使課外讀物滿足同學們的需求,學校就“我最喜愛的課外讀物”從文學、藝術、科普和其他四個類別進行了抽樣調查(每位同學只選一類),如圖是根
據調查結果繪制的兩幅不完整的統計圖.

請你根據統計圖提供的信息,解答下列問題:
(1)本次調查中,一共調查了 名同學;
(2)條形統計圖中,m= ,n= ;
(3)扇形統計圖中,藝術類讀物所在扇形的圓心角是 度;
(4)學校計劃購買課外讀物6000冊,請根據樣本數據,估計學校購買其他類讀物多少冊比較合理?
查看答案和解析>>
科目:初中數學 來源: 題型:
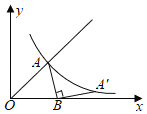
【題目】如圖,函數y=x(x≥0)的圖象與反比例函數y=![]() 的圖象交于點A,若點A繞點B(
的圖象交于點A,若點A繞點B(![]() ,0)順時針旋轉90°后,得到的點A'仍在y=
,0)順時針旋轉90°后,得到的點A'仍在y=![]() 的圖象上,則點A的坐標為_____.
的圖象上,則點A的坐標為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com