
【題目】探索與研究:
方法1:如圖(a),對(duì)任意的符合條件的直角三角形繞其銳角頂點(diǎn)旋轉(zhuǎn)90°所得,所以
∠BAE=90°,且四邊形ACFD是一個(gè)正方形,它的面積和四邊形ABFE面積相等,而四邊形ABFE面積等于Rt△BAE和Rt△BFE的面積之和,根據(jù)圖示寫出證明勾股定理的過程;
方法2:如圖(b),是任意的符合條件的兩個(gè)全等的Rt△BEA和Rt△ACD拼成的,你能根據(jù)圖示再寫一種證明勾股定理的方法嗎?

【答案】答案見解析
【解析】試題分析:根據(jù)面積相等的法則進(jìn)行計(jì)算.
試題解析:方法1:∵由圖(a)可知S正方形ACFD=S四邊形ABFE ,
∴S正方形ACFD=S⊿BAE+S⊿BFE
又∵正方形ACFD的邊長(zhǎng)為b, SRt△BAE=![]() ,SRt△BFE=
,SRt△BFE=![]()
∴b2 =![]() +
+![]()
即2b2 =c2 +(b+a)(b-a)
整理得: a2+b2=c2
方法2:如圖(b)中,Rt△BEA和Rt△ACD全等, 設(shè)CD=a,AC=b,AD=c(b>a),
則AE=a,BE=b,AB=c,EC=b-a
由圖(b),S四邊形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD
又∵SRt△BAE =![]() , SRt△ACD =
, SRt△ACD =![]() ,SRt△BEC=
,SRt△BEC=![]() ,
,
SRt△BAD=![]() ,S△BCD=
,S△BCD=![]() ,
,
∴![]() +
+![]() +
+![]() =
=![]() +
+![]()
即2ab+b(b-a)= c2 +a(b-a)
整理得: a2+b2=c2



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】 小明同學(xué)5次數(shù)學(xué)單元測(cè)試的平均成績(jī)是90分,中位數(shù)是91分,眾數(shù)是94分,則兩次最低成績(jī)之和是( )
A. 165分 B. 168分 C. 170分 D. 171分
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在一次水災(zāi)中,大約有2.5×105個(gè)人無家可歸,假如一頂帳篷占地100米2,可以放置40個(gè)床位,為了安置所有無家可歸的人,需要多少頂帳篷?這些帳篷大約要占多少地方?估計(jì)你的學(xué)校的操場(chǎng)可安置多少人?要安置這些人,大約需要多少個(gè)這樣的操場(chǎng)?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,A(0,1),M(3,2),N(4,4) , 動(dòng)點(diǎn)P從點(diǎn)A出發(fā),沿y
軸以每秒1個(gè)單位長(zhǎng)的速度向上移動(dòng),且過點(diǎn)P的直線l:y=-x+b也隨之移動(dòng),設(shè)移動(dòng)時(shí)間為 t 秒.(直線y = kx+b平移時(shí)k不變)

(1)當(dāng)t=3時(shí),求 l 的解析式;
(2)若點(diǎn)M,N位于l 的異側(cè),確定 t 的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,二次函數(shù)y=ax2+bx+c的圖象與x軸交于A、B兩點(diǎn),其中A點(diǎn)坐標(biāo)為(﹣1,0),點(diǎn)C(0,5),另拋物線經(jīng)過點(diǎn)(1,8),M為它的頂點(diǎn).
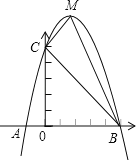
(1)求拋物線的解析式;
(2)求△MCB的面積S△MCB.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
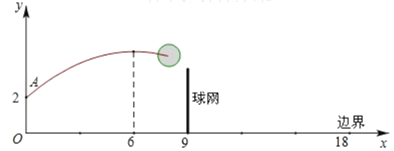
【題目】如圖,排球運(yùn)動(dòng)員站在點(diǎn)O處練習(xí)發(fā)球,將球從O點(diǎn)正上方2![]() 的A處發(fā)出,把球看成點(diǎn),其運(yùn)行的高度
的A處發(fā)出,把球看成點(diǎn),其運(yùn)行的高度![]() 與運(yùn)行的水平距離
與運(yùn)行的水平距離![]() 滿足關(guān)系式
滿足關(guān)系式![]() .已知球網(wǎng)與O點(diǎn)的水平距離為9
.已知球網(wǎng)與O點(diǎn)的水平距離為9![]() ,高度為2.43
,高度為2.43![]() ,球場(chǎng)的邊界距O點(diǎn)的水平距離為18
,球場(chǎng)的邊界距O點(diǎn)的水平距離為18![]() .
.
(1)當(dāng)![]() =2.6時(shí),求
=2.6時(shí),求![]() 與
與![]() 的關(guān)系式(不要求寫出自變量
的關(guān)系式(不要求寫出自變量![]() 的取值范圍);
的取值范圍);
(2)當(dāng)![]() =2.6時(shí),球能否越過球網(wǎng)?球會(huì)不會(huì)出界?請(qǐng)說明理由;
=2.6時(shí),球能否越過球網(wǎng)?球會(huì)不會(huì)出界?請(qǐng)說明理由;
(3)若球一定能越過球網(wǎng),又不出邊界,求二次函數(shù)中![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)﹣![]() ﹣
﹣![]() ﹣(﹣
﹣(﹣![]() )﹣
)﹣![]()
(2)9.872+(﹣![]() )+(﹣5.872)
)+(﹣5.872)
(3)(![]() ﹣
﹣![]()
![]() )÷(﹣
)÷(﹣![]() );
);
(4)![]()
![]()
(5)1.3×(﹣9.12)+(﹣7)×9.12
(6)﹣14﹣![]() ×[2﹣(﹣3)]2
×[2﹣(﹣3)]2
(7)[![]() ÷(﹣
÷(﹣![]() )+0.4×
)+0.4×![]() ]×(﹣1)5
]×(﹣1)5
(8)[1![]() ]2÷[(1﹣
]2÷[(1﹣![]() )×
)×![]() ]3.
]3.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com