
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上,
上,![]() ,連接
,連接![]() ,
,![]() .動點
.動點![]() 在
在![]() 上從點
上從點![]() 向終點
向終點![]() 勻速運動,同時,動點
勻速運動,同時,動點![]() 在射線
在射線![]() .上從點
.上從點![]() 沿
沿![]() 方向勻速運動,當點
方向勻速運動,當點![]() 運動到EF的中點時,點
運動到EF的中點時,點![]() 恰好與點
恰好與點![]() 重合,點
重合,點![]() 到達終點時,
到達終點時,![]() ,
, ![]() 同時停止運動.
同時停止運動.
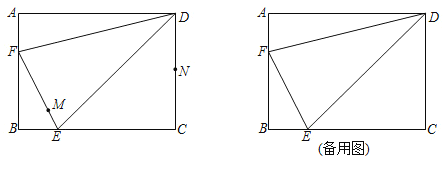
(1)求![]() 的長.
的長.
(2)設![]() ,
,![]() ,求
,求![]() 關于
關于![]() 的函數表達式,并寫出自變
的函數表達式,并寫出自變![]() 的取值范圍.
的取值范圍.
(3)連接![]() ,當
,當![]() 與
與![]() 的一邊平行時,求
的一邊平行時,求![]() 的長.
的長.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() );(3)
);(3)![]() 的值為
的值為![]() 或12
或12
【解析】
(1)由矩形的性質可得:∠B=90°,在Rt△BEF中,根據勾股定理即可求出EF的長;
(2)已知![]() ,
,![]() ,根據“當點
,根據“當點![]() 運動到EF的中點時,點
運動到EF的中點時,點![]() 恰好與點
恰好與點![]() 重合”,即可求出
重合”,即可求出![]() 關于
關于![]() 的函數表達式;
的函數表達式;
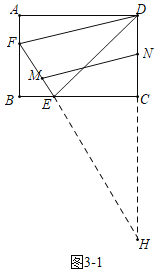
(3)如圖3-1和3-2中,延長![]() 交
交![]() 的延長線于
的延長線于![]() ,根據相似三角形的判定定理可證得
,根據相似三角形的判定定理可證得![]() ,根據相似三角形對應邊成比例可得EH,CH的長,然后分三種情況討論:①
,根據相似三角形對應邊成比例可得EH,CH的長,然后分三種情況討論:①![]() ,②
,②![]() ,③
,③![]() ,排除掉不存在的情況,繼而根據相似三角形對應邊成比例即可求解.
,排除掉不存在的情況,繼而根據相似三角形對應邊成比例即可求解.
(1)∵四邊形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)由題意得: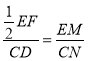 ,
,
即![]() .
.
∴![]() (
(![]() ).
).
(3)如圖,延長![]() 交
交![]() 的延長線于
的延長線于![]() .
.
∵四邊形ABCD是矩形,
∴∠B=∠ECD=∠ECH=90°,
又∵∠BEF=∠CEH,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
①如圖3-1,當![]() 時,△HMN∽△HFD,
時,△HMN∽△HFD,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
②當![]() 時,這種情形不存在.
時,這種情形不存在.
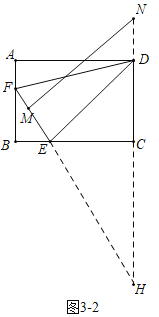
③如圖3-2中,當![]() 時,△HED∽△HMN,
時,△HED∽△HMN,
∴![]() ,即
,即![]() ,
,
∵![]() ,解得
,解得![]() ,
,
綜上所述,滿足條件的![]() 的值為
的值為![]() 或12.
或12.


 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,對角線BD所在的直線上有兩點E、F滿足BE=DF,連接AE、AF、CE、CF,如圖所示.
(1)求證:△ABE≌△ADF;
(2)試判斷四邊形AECF的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
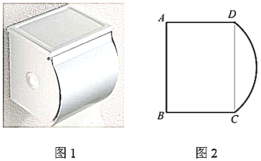
【題目】如圖1是一種紙巾盒,由盒身和圓弧蓋組成,通過圓弧蓋的旋轉來開關紙巾盒.如圖2是其側面簡化示意圖,已知矩形![]() 的長
的長![]() ,寬
,寬![]() ,圓弧蓋板側面
,圓弧蓋板側面![]() 所在圓的圓心
所在圓的圓心![]() 是矩形
是矩形![]() 的中心,繞點
的中心,繞點![]() 旋轉開關(所有結果保留小數點后一位).
旋轉開關(所有結果保留小數點后一位).
(1)求![]() 所在
所在![]() 的半徑長及
的半徑長及![]() 所對的圓心角度數;
所對的圓心角度數;
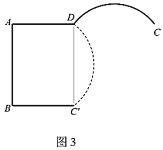
(2)如圖3,當圓弧蓋板側面![]() 從起始位置
從起始位置![]() 繞點
繞點![]() 旋轉
旋轉![]() 時,求
時,求![]() 在這個旋轉過程中掃過的的面積.
在這個旋轉過程中掃過的的面積.
參考數據:![]() ,
,![]() ,
,![]() 取3.14.
取3.14.
查看答案和解析>>
科目:初中數學 來源: 題型:
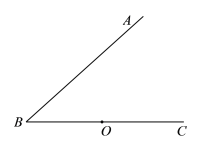
【題目】如圖,點O為∠ABC的邊![]() 上的一點,過點O作OM⊥AB于點
上的一點,過點O作OM⊥AB于點![]() ,到點
,到點![]() 的距離等于線段OM的長的所有點組成圖形
的距離等于線段OM的長的所有點組成圖形![]() .圖形W與射線
.圖形W與射線![]() 交于E,F兩點(點在點F的左側).
交于E,F兩點(點在點F的左側).
(1)過點![]() 作
作![]() 于點
于點![]() ,如果BE=2,
,如果BE=2,![]() ,求MH的長;
,求MH的長;
(2)將射線BC繞點B順時針旋轉得到射線BD,使得∠![]()
![]() ,判斷射線BD與圖形
,判斷射線BD與圖形![]() 公共點的個數,并證明.
公共點的個數,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=x+4的圖象與反比例函數y2=![]() 的圖象交于A(﹣1,a),B兩點,與x軸交于點C.
的圖象交于A(﹣1,a),B兩點,與x軸交于點C.
(1)求k.
(2)根據圖象直接寫出y1>y2時,x的取值范圍.
(3)若反比例函數y2=![]() 與一次函數y1=x+4的圖象總有交點,求k的取值.
與一次函數y1=x+4的圖象總有交點,求k的取值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】黃石市在創建國家級文明衛生城市中,綠化檔次不斷提升.某校計劃購進A,B兩種樹木共100棵進行校園綠化升級,經市場調查:購買A種樹木2棵,B種樹木5棵,共需600元;購買A種樹木3棵,B種樹木1棵,共需380元.
(1)求A種,B種樹木每棵各多少元?
(2)因布局需要,購買A種樹木的數量不少于B種樹木數量的3倍.學校與中標公司簽訂的合同中規定:在市場價格不變的情況下(不考慮其他因素),實際付款總金額按市場價九折優惠,請設計一種購買樹木的方案,使實際所花費用最省,并求出最省的費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰三角形ABC中,AB=AC=2,∠B=75°,以C為旋轉中心將△ABC順時針旋轉,當點B落在AB上點D處時,點A的對應點為E,則陰影部分面積為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,弦AB垂直平分半徑OC,垂足為D.若點P是⊙O上異于點A,B的任意一點,則∠APB=( )
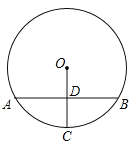
A.30°或60°B.60°或150°C.30°或150°D.60°或120°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在某一路段,規定汽車限速行駛,交通警察在此限速路段的道路上設置了監測區,其中點C、D為監測點,已知點C、D、B在同一直線上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
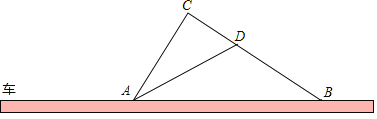
(1)求道路AB段的長(結果精確到1米)
(2)如果道路AB的限速為60千米/時,一輛汽車通過AB段的時間為90秒,請你判斷該車是否是超速,并說明理由;參考數據:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com