
【題目】如圖,在ABCD中,AB=4,AD=5,tanA=![]() ,點(diǎn)P從點(diǎn)A出發(fā),沿折線AB﹣BC以每秒1個(gè)單位長(zhǎng)度的速度向中點(diǎn)C運(yùn)動(dòng),過(guò)點(diǎn)P作PQ⊥AB,交折線AD﹣DC于點(diǎn)Q,將線段PQ繞點(diǎn)P順時(shí)針旋轉(zhuǎn)90°,得到線段PR,連接QR.設(shè)△PQR與ABCD重疊部分圖形的面積為S(平方單位),點(diǎn)P運(yùn)動(dòng)的時(shí)間為t(秒).
,點(diǎn)P從點(diǎn)A出發(fā),沿折線AB﹣BC以每秒1個(gè)單位長(zhǎng)度的速度向中點(diǎn)C運(yùn)動(dòng),過(guò)點(diǎn)P作PQ⊥AB,交折線AD﹣DC于點(diǎn)Q,將線段PQ繞點(diǎn)P順時(shí)針旋轉(zhuǎn)90°,得到線段PR,連接QR.設(shè)△PQR與ABCD重疊部分圖形的面積為S(平方單位),點(diǎn)P運(yùn)動(dòng)的時(shí)間為t(秒).
(1)當(dāng)點(diǎn)R與點(diǎn)B重合時(shí),求t的值;
(2)當(dāng)點(diǎn)P在BC邊上運(yùn)動(dòng)時(shí),求線段PQ的長(zhǎng)(用含有t的代數(shù)式表示);
(3)當(dāng)點(diǎn)R落在ABCD的外部時(shí),求S與t的函數(shù)關(guān)系式;
(4)直接寫(xiě)出點(diǎn)P運(yùn)動(dòng)過(guò)程中,△PCD是等腰三角形時(shí)所有的t值.

【答案】(1)![]() ;(2)
;(2)![]() (9﹣t);(3)①S =﹣
(9﹣t);(3)①S =﹣![]() t2+
t2+![]() t﹣
t﹣![]() ;②S=﹣
;②S=﹣![]() t2+8.③S=
t2+8.③S=![]() (9﹣t)2;(4)4或
(9﹣t)2;(4)4或![]() 或5或
或5或![]() .
.
【解析】
(1)根據(jù)題意點(diǎn)R與點(diǎn)B重合時(shí)t+![]() t=4,即可求出t的值;
t=4,即可求出t的值;
(2)根據(jù)題意運(yùn)用t表示出PQ即可;
(3)當(dāng)點(diǎn)R落在□ABCD的外部時(shí)可得出t的取值范圍,再根據(jù)等量關(guān)系列出函數(shù)關(guān)系式;
(4)根據(jù)等腰三角形的性質(zhì)即可得出結(jié)論.
解:(1)∵將線段PQ繞點(diǎn)P順時(shí)針旋轉(zhuǎn)90°,得到線段PR,
∴PQ=PR,∠QPR=90°,
∴△QPR為等腰直角三角形.
當(dāng)運(yùn)動(dòng)時(shí)間為t秒時(shí),AP=t,PQ=PQ=APtanA=![]() t.
t.
∵點(diǎn)R與點(diǎn)B重合,
∴AP+PR=t+![]() t=AB=4,
t=AB=4,
解得:t=![]() .
.
(2)當(dāng)點(diǎn)P在BC邊上時(shí),4≤t≤9,CP=9﹣t,
∵tanA=![]() ,
,
∴tanC=![]() ,sinC=
,sinC=![]() ,
,
∴PQ=CPsinC=![]() (9﹣t).
(9﹣t).
(3)①如圖1中,當(dāng)![]() <t≤3時(shí),重疊部分是四邊形PQKB.作KM⊥AR于M.
<t≤3時(shí),重疊部分是四邊形PQKB.作KM⊥AR于M.
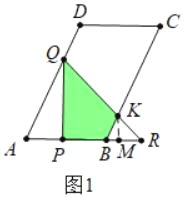
∵△KBR∽△QAR,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴KM=![]() (
(![]() t﹣4)=
t﹣4)=![]() t﹣
t﹣![]() ,
,
∴S=S△PQR﹣S△KBR=![]() ×(
×(![]() t)2﹣
t)2﹣![]() ×(
×(![]() t﹣4)(
t﹣4)(![]() t﹣
t﹣![]() )=﹣
)=﹣![]() t2+
t2+![]() t﹣
t﹣![]() .
.
②如圖2中,當(dāng)3<t≤4時(shí),重疊部分是四邊形PQKB.
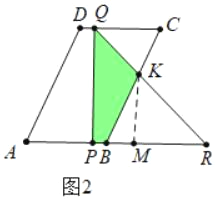
S=S△PQR﹣S△KBR=![]() ×4×4﹣
×4×4﹣![]() ×t×
×t×![]() t=﹣
t=﹣![]() t2+8.
t2+8.
③如圖3中,當(dāng)4<t<9時(shí),重疊部分是△PQK.
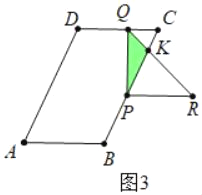
S=![]() S△PQC=
S△PQC=![]() ×
×![]() ×
×![]() (9﹣t)
(9﹣t)![]() (9﹣t)=
(9﹣t)=![]() (9﹣t)2.
(9﹣t)2.
(4)如圖4中,
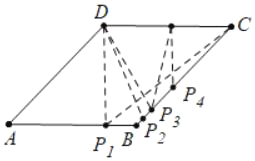
①當(dāng)DC=DP1=4時(shí),易知AP1=4,t=4.
②當(dāng)DC=DP2時(shí),CP2=2CD![]() =
=![]() ,
,
∴BP2=![]() ,
,
∴t=4+![]() =
=![]() .
.
③當(dāng)CD=CP3時(shí),t=5.
④當(dāng)CP4=DP4時(shí),CP4=2÷![]() =
=![]() ,
,
∴t=9﹣![]() =
=![]() .
.
綜上所述,滿足條件的t的值為4或![]() 或5或
或5或![]() .
.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,在四邊形![]() 中,
中,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點(diǎn),
的中點(diǎn),![]() 、
、![]() 的延長(zhǎng)線分別與
的延長(zhǎng)線分別與![]() 的延長(zhǎng)線交于點(diǎn)
的延長(zhǎng)線交于點(diǎn)![]() 、
、![]() ,則( )
,則( )
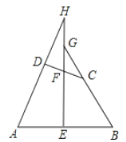
A.![]() B.
B.![]()
C.![]() D.
D.![]() 與
與![]() 的大小關(guān)系不確定
的大小關(guān)系不確定
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,D、E分別是AC、AB上的點(diǎn),BD與CE相交于點(diǎn)O,給出四個(gè)條件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四個(gè)條件中,選擇兩個(gè)可以判定△ABC是等腰三角形的方法有( )
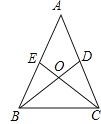
A.2種B.3種C.4種D.6種
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】有4張正面分別標(biāo)有數(shù)字﹣1,2,﹣3,4的不透明卡片,它們除數(shù)字外其余全部相同,現(xiàn)將它們背面朝上,洗勻后從4張卡片中隨機(jī)摸出一張不放回,將該卡片上的數(shù)字記為m,在隨機(jī)抽取1張,將卡片的數(shù)字即為n.
(1)請(qǐng)用列表或樹(shù)狀圖的方式把(m,n)所有的結(jié)果表示出來(lái).
(2)求選出的(m,n)在二、四象限的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(1)如圖(a)所示點(diǎn)D是等邊![]() 邊BA上一動(dòng)點(diǎn)(點(diǎn)D與點(diǎn)B不重合),連接DC,以DC為邊在BC上方作等邊
邊BA上一動(dòng)點(diǎn)(點(diǎn)D與點(diǎn)B不重合),連接DC,以DC為邊在BC上方作等邊![]() ,連接AF.你能發(fā)現(xiàn)線段AF與BD之間的數(shù)量關(guān)系嗎?并證明.
,連接AF.你能發(fā)現(xiàn)線段AF與BD之間的數(shù)量關(guān)系嗎?并證明.
(2)如圖(b)所示當(dāng)動(dòng)點(diǎn)D運(yùn)動(dòng)至等邊![]() 邊BA的延長(zhǎng)線上時(shí),其他作法與(1)相同,猜想AF與BD在(1)中的結(jié)論是否仍然成立?(直接寫(xiě)出結(jié)論)
邊BA的延長(zhǎng)線上時(shí),其他作法與(1)相同,猜想AF與BD在(1)中的結(jié)論是否仍然成立?(直接寫(xiě)出結(jié)論)
(3)①如圖(c)所示,當(dāng)動(dòng)點(diǎn)D在等邊![]() 邊BA上運(yùn)動(dòng)時(shí)(點(diǎn)D與點(diǎn)B不重合),連接DC,以DC為邊在BC上方、下方分別作等邊
邊BA上運(yùn)動(dòng)時(shí)(點(diǎn)D與點(diǎn)B不重合),連接DC,以DC為邊在BC上方、下方分別作等邊![]() 和等邊
和等邊![]() ,連接AF、
,連接AF、![]() ,探究AF、
,探究AF、![]() 與AB有何數(shù)量關(guān)系?并證明.
與AB有何數(shù)量關(guān)系?并證明.
②如圖(d)所示,當(dāng)動(dòng)點(diǎn)D在等邊![]() 邊BA的延長(zhǎng)線上運(yùn)動(dòng)時(shí),其他作法與(3)①相同,①中的結(jié)論是否成立?若不成立,是否有新的結(jié)論?并證明.
邊BA的延長(zhǎng)線上運(yùn)動(dòng)時(shí),其他作法與(3)①相同,①中的結(jié)論是否成立?若不成立,是否有新的結(jié)論?并證明.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四邊形![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊上一點(diǎn),
邊上一點(diǎn),![]() ,
,![]() ,垂足為點(diǎn)
,垂足為點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() .
.
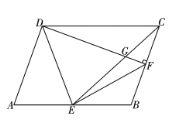
(1)四邊形![]() 是平行四邊形嗎?說(shuō)明理由;
是平行四邊形嗎?說(shuō)明理由;
(2)求證:![]() ;
;
(3)若點(diǎn)![]() 是
是![]() 邊的中點(diǎn),求證:
邊的中點(diǎn),求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,在![]() 中,
中,![]() ,
,![]() ,以A為圓心,任意長(zhǎng)為半徑畫(huà)弧分別交AB、AC于點(diǎn)M和N再分別以MN為圓心,大于
,以A為圓心,任意長(zhǎng)為半徑畫(huà)弧分別交AB、AC于點(diǎn)M和N再分別以MN為圓心,大于![]() 的長(zhǎng)為半徑畫(huà)弧,兩弧交于點(diǎn)P,連接AP并延長(zhǎng)交BC于點(diǎn)D,則下列說(shuō)法中正確的有________.
的長(zhǎng)為半徑畫(huà)弧,兩弧交于點(diǎn)P,連接AP并延長(zhǎng)交BC于點(diǎn)D,則下列說(shuō)法中正確的有________.
①AD是![]() 的平分線;②
的平分線;②![]() ;③點(diǎn)D在AB的中垂線上;④
;③點(diǎn)D在AB的中垂線上;④![]()

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
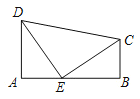
【題目】如圖,四邊形![]() 中,
中,![]() .動(dòng)點(diǎn)
.動(dòng)點(diǎn)![]() 從
從![]() 點(diǎn)出發(fā),以
點(diǎn)出發(fā),以![]() 的速度向
的速度向![]() 點(diǎn)移動(dòng),設(shè)移動(dòng)的時(shí)間為
點(diǎn)移動(dòng),設(shè)移動(dòng)的時(shí)間為![]() 秒.
秒.
(1)當(dāng)![]() 為何值時(shí),點(diǎn)
為何值時(shí),點(diǎn)![]() 在線段
在線段![]() 的垂直平分線上?
的垂直平分線上?
(2)在(1)的條件下,判斷![]() 與
與![]() 的位置關(guān)系,并說(shuō)明理由.
的位置關(guān)系,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,點(diǎn)A在半徑為20的圓O上,以O(shè)A為一條對(duì)角線作矩形OBAC,設(shè)直線BC交圓O于D、E兩點(diǎn),若OC=12,則線段CE、BD的長(zhǎng)度差是_____.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com