
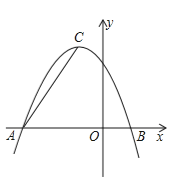
【題目】在平面直角坐標系中,拋物線![]() 與
與![]() 軸的兩個交點分別是
軸的兩個交點分別是![]() 、
、![]() ,
,![]() 為頂點.
為頂點.
(1)求![]() 、
、![]() 的值和頂點
的值和頂點![]() 的坐標;
的坐標;
(2)在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 是以
是以![]() 為斜邊的直角三角形?若存在,求出點
為斜邊的直角三角形?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ,
,![]() ,(-1,4);(2)在y軸上存在點D (0,3)或D (0,1),使△ACD是以AC為斜邊的直角三角形
,(-1,4);(2)在y軸上存在點D (0,3)或D (0,1),使△ACD是以AC為斜邊的直角三角形
【解析】
(1)把A(-3,0),B(1,0)代入![]() 解方程組即可得到結論;
解方程組即可得到結論;
(2)過C作CE⊥y軸于E,根據函數的解析式求得C(-1,4),得到CE=1,OE=4,設![]() ,得到
,得到![]() ,根據相似三角形的性質即可得到結論.
,根據相似三角形的性質即可得到結論.
(1)把A(3,0)、B(1,0)分別代入![]() ,
,
![]() ,
,
解得:![]() ,
,![]() ,
,
則該拋物線的解析式為:![]() ,
,
∵![]() ,
,
所以頂點![]() 的坐標為(
的坐標為(![]() ,
,![]() );
);
故答案為:![]() ,
,![]() ,頂點
,頂點![]() 的坐標為(
的坐標為(![]() ,
,![]() );
);
(2)如圖1,過點![]() 作
作![]() ⊥
⊥![]() 軸于點
軸于點![]() ,
,

假設在![]() 軸上存在滿足條件的點
軸上存在滿足條件的點![]() ,
,
設![]() (0,
(0,![]() ),則
),則![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由∠![]() 90
90![]() 得∠1
得∠1![]() ∠2
∠2![]() 90
90![]() ,
,
又∵∠2![]() ∠3
∠3![]() 90
90![]() ,
,
∴∠3![]() ∠1,
∠1,
又∵∠CED![]() ∠DOA
∠DOA![]() 90
90![]() ,
,
∴△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
則![]() ,
,
變形得![]() ,
,
解得![]() ,
,![]() .
.
綜合上述:在y軸上存在點![]() (0,3)或
(0,3)或![]() (0,1),使△ACD是以AC為斜邊的直角三角形.
(0,1),使△ACD是以AC為斜邊的直角三角形.


科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系xOy中,A(2,1),B(3,﹣1),C(﹣2,1),D(0,2).已知線段AB繞著點P逆時針旋轉得到線段CD,其中C是點A的對應點.
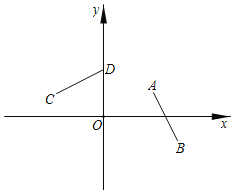
(1)用尺規作圖的方法確定旋轉中心P,并直接寫出點P的坐標;(要求保留作圖痕跡,不寫作法)
(2)若以P為圓心的圓與直線CD相切,求⊙P的半徑
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形ABCD和矩形EFGO在平面直角坐標系中,點B,F的坐標分別為(-4,4),(2,1).若矩形ABCD和矩形EFGO是位似圖形,點P(點P在GC上)是位似中心,則點P的坐標為( )
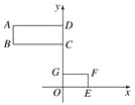
A. (0,3)
B. (0,2.5)
C. (0,2)
D. (0,1.5)
查看答案和解析>>
科目:初中數學 來源: 題型:
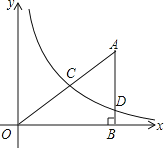
【題目】如圖,在平面直角坐標系中,![]() 為坐標原點,
為坐標原點,![]() 的邊
的邊![]() 垂直于
垂直于![]() 軸,垂足為點
軸,垂足為點![]() ,反比例函數
,反比例函數![]() 的圖象經過
的圖象經過![]() 的中點
的中點![]() ,且與
,且與![]() 相交于點
相交于點![]() .
.
(1)求反比例函數![]() 的解析式;
的解析式;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
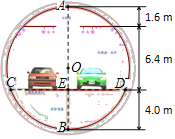
【題目】如圖,是一張盾構隧道斷面結構圖.隧道內部為以O為圓心,AB為直徑的圓.隧道內部共分為三層,上層為排煙道,中間為行車隧道,下層為服務層.點A到頂棚的距離為1.6m,頂棚到路面的距離是6.4m,點B到路面的距離為4.0m.請求出路面CD的寬度.(精確到0.1m)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為加快城鄉對接,建設美麗鄉村,某地區對A、B兩地間的公路進行改建,如圖,A,B兩地之間有一座山.汽車原來從A地到B地需途經C地沿折線ACB行駛,現開通隧道后,汽車可直接沿直線AB行駛,已知BC=80千米,∠A=45°,∠B=30°.
(1)開通隧道前,汽車從A地到B地要走多少千米?
(2)開通隧道后,汽車從A地到B地可以少走多少千米?(結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
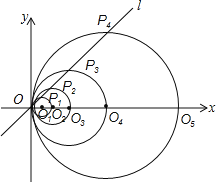
【題目】如圖,在平面直角坐標系中,直線l的函數表達式為y=x,點O1的坐標為(1,0),以O1為圓心,O1O為半徑畫圓,交直線l于點P1,交x軸正半軸于點O2,以O2為圓心,O2O為半徑畫圓,交直線l于點P2,交x軸正半軸于點O3,以O3為圓心,O3O為半徑畫圓,交直線l于點P3,交x軸正半軸于點O4;…按此做法進行下去,其中![]() 的長為_____.
的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點B(0,2),A(﹣6,﹣1)在反比例函數![]() 的圖象上,作射線AB,再將射線AB繞點A逆時針旋轉45°后,交反比例函數
的圖象上,作射線AB,再將射線AB繞點A逆時針旋轉45°后,交反比例函數![]() 圖象于點C,則點C的坐標為_____.
圖象于點C,則點C的坐標為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是弧AB的中點,弦CD與AB相交于E.
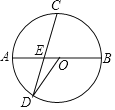
(1)若∠AOD=45°,求證:CE=![]() ED;(2)若AE=EO,求tan∠AOD的值.
ED;(2)若AE=EO,求tan∠AOD的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com