
已知:拋物線![]() 與x軸交于點(diǎn)A(
與x軸交于點(diǎn)A(![]() ,0)、B(
,0)、B(![]() ,0)(A在B的左側(cè)),與y軸交于點(diǎn)C.
,0)(A在B的左側(cè)),與y軸交于點(diǎn)C.
(1)若m>1,△ABC的面積為6,求拋物線的解析式;
(2)點(diǎn)D在x軸下方,是(1)中的拋物線上的一個(gè)動(dòng)點(diǎn),且在該拋物線對(duì)稱軸的左側(cè),作DE∥x軸與拋物線交于另一點(diǎn)E,作DF⊥x軸于F,作EG⊥x軸于點(diǎn)G,求矩形DEGF周長(zhǎng)的最大值;
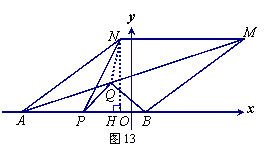
(3)若m<0,以AB為一邊在x軸上方做菱形ABMN(∠NAB為銳角), P是AB邊的中點(diǎn),Q是對(duì)角線AM上一點(diǎn),若![]() ,
,![]() ,當(dāng)菱形ABMN的面積最大時(shí),求點(diǎn)A的坐標(biāo).
,當(dāng)菱形ABMN的面積最大時(shí),求點(diǎn)A的坐標(biāo).
解:∵ 拋物線與x軸交于點(diǎn)A(x1,0)、B(x2,0),
∴ x1、x2是關(guān)于x的方程![]() 的解.
的解.
解方程,得![]() 或
或![]() .
.
(1)∵ A在B 的左側(cè),m>1,
∴![]() ,
,![]() .
.
 ∴ AB=m-1.
∴ AB=m-1.
拋物線與y軸交于C(0,m)點(diǎn).
|
|
|
|
|
∴ 拋物線解析式為![]() .
.
(2)∵ 點(diǎn)D在(1)中的拋物線上,
∴ 設(shè)D(t, ![]() )(
)(![]() ).
).
∴ F(t,0),DF=![]() .
.
又拋物線對(duì)稱軸是直線![]() ,DE與拋物線對(duì)稱軸交點(diǎn)記為R(如圖12),
,DE與拋物線對(duì)稱軸交點(diǎn)記為R(如圖12),
∴ DR=![]() ,DE=
,DE=![]() .
.
設(shè)矩形DEGF的周長(zhǎng)為L(zhǎng),則 L=2(DF+DE).
∴ L =2(![]() +
+![]() )
)
=![]()
=![]() .
.
∵ ![]() ,
,
∴ 當(dāng)且僅當(dāng)![]() 時(shí),L有最大值.
時(shí),L有最大值.
當(dāng)![]() 時(shí),L最大=
時(shí),L最大=![]() .
.
 ∴ 矩形周長(zhǎng)的最大值為
∴ 矩形周長(zhǎng)的最大值為![]() .
.
(3)∵ A在B 的左側(cè),m<0,
∴![]() ,
,![]() .
.
∴ AB=1-m.
如圖13,作NH⊥AB于H,連結(jié)QN.
在Rt△AHN中, ![]()
![]() .
.
設(shè)AH=4k(k>0), 則AN=5k,NH=3k.
∴ AP=![]() =
=![]() =
=![]() ,PH=AH -AP=
,PH=AH -AP=![]() =
=![]() ,PN=
,PN=![]() =
=![]() .
.
∵ 菱形ABMN是軸對(duì)稱圖形,
∴ QN=QB.
∴ PQ+QN = PQ+QB=6.
∵ PQ+QN≥PN(當(dāng)且僅當(dāng)P、Q、N三點(diǎn)共線時(shí),等號(hào)成立).
∴ ![]()
![]() ,
,
解得 k≤![]() .
.
∵ S菱形ABMN=AB·NH=15 k2≤48.
∴ 當(dāng)菱形面積取得最大值48時(shí),k=![]() .
.
此時(shí)AB=5k=1-m =![]() .
.
解得 m=1-![]() .
.
∴ A點(diǎn)的坐標(biāo)為(1-![]() ,0).
,0).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 拋物線y=ax2+bx+c的圖象如圖所示,已知該拋物線與x軸交于A、B兩點(diǎn),頂點(diǎn)為C,
拋物線y=ax2+bx+c的圖象如圖所示,已知該拋物線與x軸交于A、B兩點(diǎn),頂點(diǎn)為C,查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:期末題 題型:解答題
 與x軸交于A,B兩點(diǎn),與y軸交于點(diǎn)C,經(jīng)過B,C兩點(diǎn)的直線是
與x軸交于A,B兩點(diǎn),與y軸交于點(diǎn)C,經(jīng)過B,C兩點(diǎn)的直線是 ,連結(jié)AC.
,連結(jié)AC.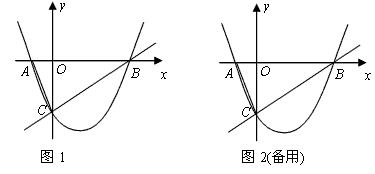
 的頂點(diǎn)坐標(biāo)是
的頂點(diǎn)坐標(biāo)是 ]
] 查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
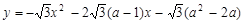 與x軸交于
與x軸交于查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com