
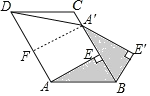
【題目】如圖,已知在ABCD中,AE⊥BC于點E,以點B為中心,取旋轉角等于∠ABC,把△BAE順時針旋轉,得到△BA′E′,連接DA′.若∠ADC=60°,AD=5,DC=4,則DA′的大小為( )

A. 1 B. ![]() C.
C. ![]() D. 2
D. 2![]()
【答案】C
【解析】
過A′作A′F⊥AD,由AE⊥BC可得AE=A′F,根據平行四邊形的性質可知AB=CD=4,∠ABC=∠ADC=60°,進而可求出BE和AE的長,根據旋轉的性質可得AB=A′B,進而可求出A′E的長,即可求出AF的長,進而求出DF的長,利用勾股定理求出DA′的長即可.
如圖:過A′作A′F⊥AD,
∵四邊形ABCD為平行四邊形,AE⊥BC,A′F⊥AD,
∴AE=A′F,
∵四邊形ABCD為平行四邊形,
∴AB=CD=4,∠ABC=∠ADC=60°,
∴∠BAE=30°,
∴BE=![]() AB=2,AE=A′F=
AB=2,AE=A′F=![]() =2
=2![]() ,
,
∵旋轉角等于∠ABC,把△BAE順時針旋轉,得到△BA′E′,
∴A′B在線段BC上,且A′B=AB=5,
∴A′E=A′B-BE=5-2=3,
∴AF=A′E=3,
∴DF=DA-AF=5-3=2,
在Rt△A′FD中,由勾股定理可得A′D=A′F2+DF2=![]() =
=![]() ,
,
故選C.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,用兩個邊長為15![]() 的小正方形拼成一個大的正方形,
的小正方形拼成一個大的正方形,
(1)求大正方形的邊長?
(2)若沿此大正方形邊的方向剪出一個長方形,能否使剪出的長方形紙片的長寬之比為4:3,且面積為720cm2?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=CB,∠ABC=90°,F為AB延長線上一點,點E在BC上,且AE=CF.

(1)求證:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AB=AC,D為△ABC所在平面內的一點,過D作DE∥AB,DF∥AC分別交直線AC,直線AB于點E,F.
(1)如圖1,當點D在線段BC上時,通過觀察分析線段DE、DF、AB之間的數量關系,并說明理由;
(2)如圖2,當點D在直線BC上,其他條件不變時,試猜想線段DE、DF、AB之間的數量關系(請直接寫出等式,不需證明);
(3)如圖3,當點D是△ABC內一點,過D作DE∥AB,DF∥AC分別交直線AC,直線AB和直線BC于E、F和G. 試猜想線段DE、DF、DG與AB之間的數量關系(請直接寫出等式,不需證明).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:我們在學習二次根式時,式子![]() 有意義,則x≥0;式子
有意義,則x≥0;式子![]() 有意義,則x≤0;若式子
有意義,則x≤0;若式子![]() +
+![]() 有意義,求x的取值范圍. 這個問題可以轉化為不等式組來解決,即求關于x的不等式組x≥0,x≤0的解集,解這個不等式組,得x=0. 請你運用上述的數學方法解決下列問題:
有意義,求x的取值范圍. 這個問題可以轉化為不等式組來解決,即求關于x的不等式組x≥0,x≤0的解集,解這個不等式組,得x=0. 請你運用上述的數學方法解決下列問題:
(1)式子![]() +
+![]() 有意義,求x的取值范圍;
有意義,求x的取值范圍;
(2)已知y=![]() +
+![]() -3,求
-3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年初,由于新冠肺炎的影響,我們不能去學校上課,但是我們“停課不停學”.所以學校派王老師開車從學校出發前往太陽鄉修善村給學生送新書,行駛一段時間后,因車子出故障,途中耽擱了一段時間,車子修好后,加速前行,到達修善村后給學生發完新書,然后勻速開車回到學校.其中![]() 表示王老師從學校出發后的時間,
表示王老師從學校出發后的時間,![]() 表示王老師離學校的距離,下面能反映
表示王老師離學校的距離,下面能反映![]() 與
與![]() 的函數關系的大致圖象是( )
的函數關系的大致圖象是( )
A.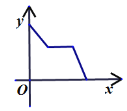 B.
B.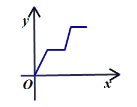
C.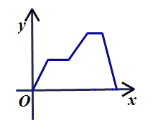 D.
D.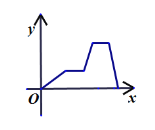
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人以相同路線前往距離單位10km的培訓中心參加學習.圖中l甲、l乙分別表示甲、乙兩人前往目的地所走的路程S(km)隨時間t(分)變化的函數圖象.以下說法:
①乙比甲提前12分鐘到達; ②甲的平均速度為15千米/小時;
③乙走了8km后遇到甲; ④乙出發6分鐘后追上甲.
其中正確的有_____________(填所有正確的序號).
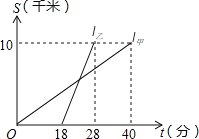
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】水果商在批發市場按每千克1.5元批發了若干千克的西瓜進城出售,為了方面他帶了一些零錢備用.他先按市場價售出一些后,又降價出售.售出西瓜的重量![]() (千克)與他手中持有的錢數
(千克)與他手中持有的錢數![]() (元)(含備用零錢)的關系如圖所示,結合圖象回答下列問題:
(元)(含備用零錢)的關系如圖所示,結合圖象回答下列問題:
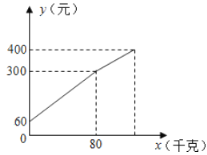
(1)水果商自帶的零錢是多少?
(2)降價前他每千克西瓜出售的價格是多少?
(3)隨后他按每千克下降0.5元的價格將剩余的西瓜售完,這時他手中的錢(含備用零錢)是400元,他一共批發了多少千克的西瓜?
(4)這個水果商一共賺了多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在長方形ABCD中,AD=6,AB=4,點E、G、H、F分別在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,點P是直線EF、GH之間任意一點,連結PE、PF、PG、PH,則△PEF和△PGH的面積和為( )

A. 5 B. 6
C. 7 D. 8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com