
小明對直角三角形很感興趣. △ABC中,∠ACB=90°,D是AB上任意一點,連接DC,作DE⊥DC,EA⊥AC,DE與AE交于點E.請你跟著他一起解決下列問題: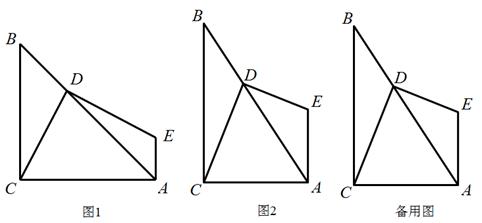
(1)如圖1,若△ABC是等腰直角三角形,則DE,DC有什么數量關系?請給出證明.
(2)如果換一個直角三角形,如圖2,∠CBA=30°,則DE,DC又有什么數量關系?請給出證明.
(3)由(1)、(2)這兩種特殊情況,小明提出問題:如果直角三角形ABC中,BC=mAC,那DE, DC有什么數量關系?請給出證明.
(1)DE=DC,證明見解析;(2)DC=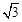 DE,證明見解析;(2)DC=
DE,證明見解析;(2)DC=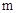 DE,證明見解析.
DE,證明見解析.
解析試題分析:(1) 過點D作DF⊥AC,DG⊥AE于點G,通過證明△CDF≌△EDG而得出結論;
(2) 過點D作DF⊥AC,DG⊥AE于點G,應用銳角三角函數定義和.特殊角的三角函數值,通過證明△CDF∽△EDG而得出結論;
(3) 過點D作DF⊥AC,DG⊥AE于點G,根據BC=mAC,通過證明△CDF∽△EDG而得出結論.
試題解析:(1)DE=DC,證明如下:
如圖,過點D作DF⊥AC,DG⊥AE于點G,
由EA⊥AC可知四邊形AGDF為矩形,∴DG="FA."
∵DF∥BC,△ABC是等腰直角三角形,∴DF=AF,即DG=DF.
又∵DE⊥DC,∴∠CDE-∠EDF=∠FDG-∠EDF,即∠CDF=∠EDG.
∴△CDF≌△EDG. ∴DE=DC.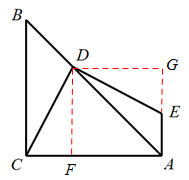
(2)DC=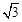 DE,證明如下:
DE,證明如下:
如圖,過點D作DF⊥AC,DG⊥AE于點G,
由EA⊥AC可知四邊形AGDF為矩形,∴DG=FA.
∵DE⊥DC,∴∠CDE-∠EDF=∠FDG-∠EDF,即∠CDF=∠EDG. ∴△CDF∽△EDG. ∴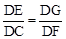 .
.
又∵△ADF∽△ABC,∴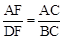 .
.
∵∠CBA=30°,∴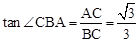 .
.
∴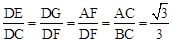 .∴DC=
.∴DC=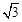 DE.
DE.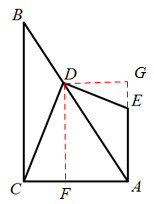
(3) DC=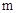 DE.證明如下:
DE.證明如下:
如圖,過點D作DF⊥AC,DG⊥AE于點G,
由EA⊥AC可知四邊形AGDF為矩形,∴DG=FA.
∵DE⊥DC,∴∠CDE-∠EDF=∠FDG-∠EDF,即∠CDF=∠EDG. ∴△CDF∽△EDG. ∴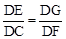 .
.
又∵△ADF∽△ABC,∴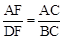 .
.
∵BC=mAC,∴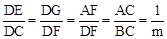 .∴DC=
.∴DC=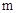 DE.
DE.
考點:1.矩形的判定和性質;2. 等腰直角三角形的性質;3.全等三角形的判定和性質;4.銳角三角函數定義;5.特殊角的三角函數值;6.相似三角形的判定和性質.


科目:初中數學 來源: 題型:解答題
已知:△ABD和△CBD關于直線BD對稱(點A的對稱點是點C),點E、F分別是線段BC和線段BD上的點,且點F在線段EC的垂直平分線上,連接AF、AE,AE交BD于點G.
(1)如圖l,求證:∠EAF=∠ABD;
(2)如圖2,當AB=AD時,M是線段AG上一點,連接BM、ED、MF,MF的延長線交ED于點N,∠MBF= ∠BAF,AF=
∠BAF,AF= AD,請你判斷線段FM和FN之間的數量關系,并證明你的判斷是正確的.
AD,請你判斷線段FM和FN之間的數量關系,并證明你的判斷是正確的.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在□ABCD中,E是AB的中點,ED和AC相交于點F,過點F作FG∥AB,交AD于點G.
(1)求證:AB=3FG;
(2)若AB:AC=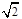 :
: ,求證:
,求證: .
.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
理解與應用
小明在學習相似三角形時,在北京市義務教育課程改革實驗教材第17冊書,第37頁遇到這樣一道題:
如圖1,在△ABC中,P是邊AB上的一點,聯結CP.
要使△ACP∽△ABC,還需要補充的一個條件是____________,或_________.
請回答:
(1)小明補充的條件是____________________,或_________________.
(2)請你參考上面的圖形和結論,探究、解答下面的問題:
如圖2,在△ABC中,∠A=60°,AC2= AB2+AB.BC.求∠B的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
探究一:如圖1,已知正方形ABCD,E、F分別是BC、AB上的兩點,且AE⊥DF.小明經探究,發現AE=DF.請你幫他寫出證明過程.
探究二:如圖2,在矩形ABCD中,AB=3,BC=4,E、G分別在邊BC、AD上,F、H分別在邊AB、CD上,且GE⊥FH.小明發現,GE與FH并不相等,請你幫他求出 的值.
的值. 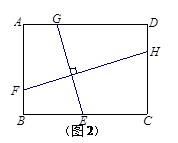
探究三:小明思考這樣一個問題:如圖3,在正方形ABCD中,若E、G分別在邊BC、AD上,F、H分別在邊AB、CD上,且GE=FH,試問:GE⊥FH是否成立?若一定成立,請給予證明;若不一定成立,請畫圖并作出說明.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知∠AOB=90°,OM是∠AOB的平分線,按以下要求解答問題:
(1)如圖1,將三角板的直角頂點P在射線OM上移動,兩直角邊分別與OA,OB交于點C,D.
①比較大小:PC______PD. (選擇“>”或“<”或“=”填空);
②證明①中的結論.
(2)將三角板的直角頂點P在射線OM上移動,一直角邊與邊OA交于點C,且OC=1,另一直角邊與直線OB,直線OA分別交于點D,E,當以P,C,E為頂點的三角形與△OCD相似時,試求 的長.(提示:請先在備用圖中畫出相應的圖形,再求
的長.(提示:請先在備用圖中畫出相應的圖形,再求 的長).
的長). 
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
以平面上一點O為直角頂點,分別畫出兩個直角三角形,記作△AOB和△COD,其中∠ABO=∠DCO=30°.
(1)點E、F、M分別是AC、CD、DB的中點,連接EF和FM.
①如圖1,當點D、C分別在AO、BO的延長線上時, =_______;
=_______;
②如圖2,將圖1中的△AOB繞點O沿順時針方向旋轉 角(
角( ),其他條件不變,判斷
),其他條件不變,判斷 的值是否發生變化,并對你的結論進行證明;
的值是否發生變化,并對你的結論進行證明;
(2)如圖3,若BO= ,點N在線段OD上,且NO=3.點P是線段AB上的一個動點,在將△AOB繞點O旋轉的過程中,線段PN長度的最小值為_______,最大值為_______.
,點N在線段OD上,且NO=3.點P是線段AB上的一個動點,在將△AOB繞點O旋轉的過程中,線段PN長度的最小值為_______,最大值為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
觀察計算:
當 ,
, 時,
時, 與
與 的大小關系是_________________.
的大小關系是_________________.
當 ,
, 時,
時, 與
與 的大小關系是_________________.
的大小關系是_________________.
探究證明:
如圖所示, 為圓O的內接三角形,
為圓O的內接三角形, 為直徑,過C作
為直徑,過C作 于D,設
于D,設 ,BD=b.
,BD=b.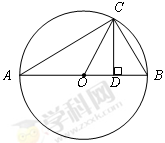
(1)分別用 表示線段OC,CD;
表示線段OC,CD;
(2)探求OC與CD表達式之間存在的關系(用含a,b的式子表示).
歸納結論:
根據上面的觀察計算、探究證明,你能得出 與
與 的大小關系是:______________.
的大小關系是:______________.
實踐應用:
要制作面積為4平方米的長方形鏡框,直接利用探究得出的結論,求出鏡框周長的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
將矩形ABCD紙片沿對角線AC剪開,得到△ABC和△A′C′D,如圖1所示,將△A′C′D的頂點A′與點A重合,并繞點A按逆時針方向旋轉,使點D、A(A′)、B在同一條直線上,如圖2所示,觀察圖2可知:與BC相等的線段是______,∠CAC′=______°。
問題探究:如圖3,△ABC中,AG⊥BC于點G,以A為直角頂點,分別以AB、AC為直角邊,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,過點E、F作射線GA的垂線,垂足分別為P、Q,試探究EP與FQ之間的數量關系,并證明你的結論.,
拓展延伸:如圖4,△ABC中,AG⊥BC于點G,分別以AB、AC為一邊向△ABC外作矩形ABME和矩形ACNF,射線GA交EF于點H,若AB=kAE,AC=kAF,試探究HE與HF之間的數量關系,并說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com