
【題目】如圖所示,在△ABC中,∠CAB=70°,現(xiàn)將△ABC繞點(diǎn)A順時(shí)針旋轉(zhuǎn)一定角度后得到△AB′C′,連接BB′,若BB′∥AC′,則∠CAB′的度數(shù)為( ) 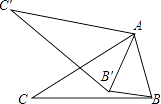
A.20°
B.25°
C.30°
D.40°
【答案】C
【解析】解:由旋轉(zhuǎn)的性質(zhì)得:∠C′AB′=∠CAB=70°,AB′=AB, ∴∠AB′B=∠ABB′,
∵BB′∥AC′,
∴∠AB′B=∠C′AB′=70°,
∴∠ABB′=70°,
∴∠BAB′=180°﹣70°﹣70°=40°,
∴∠CAB′=∠CAB﹣∠BAB′=70°﹣40°=30°;
故選:C.
由旋轉(zhuǎn)的性質(zhì)得出∠C′AB′=∠CAB=70°,AB′=AB,得出∠AB′B=∠ABB′,由平行線(xiàn)得出∠AB′B=∠C′AB′=70°,由三角形內(nèi)角和求出∠BAB′,即可得出∠CAB′的度數(shù).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,D為△ABC內(nèi)一點(diǎn),CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,則BD的長(zhǎng)為( )

A. 1 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,二次函數(shù)y=ax2+bx+c的圖象開(kāi)口向上,對(duì)稱(chēng)軸為直線(xiàn)x=1,圖象經(jīng)過(guò)(3,0),下列結(jié)論中,正確的一項(xiàng)是( ) 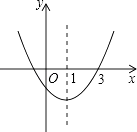
A.abc<0
B.4ac﹣b2<0
C.a﹣b+c<0
D.2a+b<0
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,一個(gè)四邊形紙片ABCD,∠B=∠D=90°,把紙片按如圖所示折疊,使點(diǎn)B落在AD邊上的B'點(diǎn),AE是折痕。

(1)試判斷B'E與DC的位置關(guān)系并說(shuō)明理由。
(2)如果∠C=130°,求∠AEB的度數(shù)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】閱讀下面材料:
在數(shù)學(xué)課上,老師提出如下問(wèn)題:
尺規(guī)作圖:作對(duì)角線(xiàn)等于已知線(xiàn)段的菱形.
 已知:兩條線(xiàn)段a、b.
已知:兩條線(xiàn)段a、b.
求作:菱形AMBN,使得其對(duì)角線(xiàn)分別等于b和2a.
尺規(guī)作圖:作對(duì)角線(xiàn)等于已知線(xiàn)段的菱形.
 已知:兩條線(xiàn)段a、b.
已知:兩條線(xiàn)段a、b.
求作:菱形AMBN,使得其對(duì)角線(xiàn)分別等于b和2a.
小軍的作法如下:
如圖
(1)畫(huà)一條線(xiàn)段AB等于b;
(2)分別以A、B為圓心,大于![]() AB的長(zhǎng)為半徑,
AB的長(zhǎng)為半徑,
在線(xiàn)段AB的上下各作兩條弧,兩弧相交于P、Q兩點(diǎn);
(3)作直線(xiàn)PQ交AB于O點(diǎn);
(4)以O點(diǎn)為圓心,線(xiàn)段a的長(zhǎng)為半徑作兩條弧,交直線(xiàn)PQ于M、N兩點(diǎn),連接AM、AN、BM、BN.所以四邊形AMBN就是所求的菱形.
如圖
(1)畫(huà)一條線(xiàn)段AB等于b;
(2)分別以A、B為圓心,大于![]() AB的長(zhǎng)為半徑,
AB的長(zhǎng)為半徑,
在線(xiàn)段AB的上下各作兩條弧,兩弧相交于P、Q兩點(diǎn);
(3)作直線(xiàn)PQ交AB于O點(diǎn);
(4)以O點(diǎn)為圓心,線(xiàn)段a的長(zhǎng)為半徑作兩條弧,交直線(xiàn)PQ于M、N兩點(diǎn),連接AM、AN、BM、BN.所以四邊形AMBN就是所求的菱形.
老師說(shuō):“小軍的作法正確.”
該上面尺規(guī)作圖作出菱形AMBN的依據(jù)是_______________________________

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,在矩形ABCD中,AB=8,BC=4.在AD上取一點(diǎn)E,AE=1,點(diǎn)F是AB邊上的一個(gè)動(dòng)點(diǎn),以EF為一邊作菱形EFMN,使點(diǎn)N落在CD邊上,點(diǎn)M落在矩形ABCD內(nèi)或其邊上.若AF=x,△BFM的面積為S.
(1)當(dāng)四邊形EFMN是正方形時(shí),求x的值;

(2)當(dāng)四邊形EFMN是菱形時(shí),求S與x的函數(shù)關(guān)系式;

(3)當(dāng)x= 時(shí),△BFM的面積S最大;當(dāng)x= 時(shí),△BFM的面積S最小;
(4)在△BFM的面積S由最大變?yōu)樽钚〉倪^(guò)程中,請(qǐng)直接寫(xiě)出點(diǎn)M運(yùn)動(dòng)的路線(xiàn)長(zhǎng): 。


查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下面是“求作∠AOB的角平分線(xiàn)”的尺規(guī)作圖過(guò)程.
已知:如圖,鈍角∠AOB.
求作:∠AOB的角平分線(xiàn).
作法:
①在OA和OB上,分別截取OD、OE,使OD=OE;
②分別以D、E為圓心,大于![]() DE的長(zhǎng)為半徑作弧,在∠AOB內(nèi),兩弧交于點(diǎn)C;
DE的長(zhǎng)為半徑作弧,在∠AOB內(nèi),兩弧交于點(diǎn)C;
③作射線(xiàn)OC.
所以射線(xiàn)OC就是所求作的∠AOB的角平分線(xiàn).
請(qǐng)回答:該尺規(guī)作圖的依據(jù)是__.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】閱讀下列兩則材料:
材料一:我們可以將任意三位數(shù)記為![]() (其中a,b,c分別表示該數(shù)百位數(shù)字、十位數(shù)字和個(gè)位數(shù)字,且a≠0),顯然
(其中a,b,c分別表示該數(shù)百位數(shù)字、十位數(shù)字和個(gè)位數(shù)字,且a≠0),顯然![]() =100a+10b+c.
=100a+10b+c.
材料二:若一個(gè)三位數(shù)的百位數(shù)字、十位數(shù)字和個(gè)位數(shù)字均不為0,則稱(chēng)之為原始數(shù),比如123就是一個(gè)原始數(shù),將原始數(shù)的三個(gè)數(shù)位上的數(shù)字交換順序,可產(chǎn)生出5個(gè)原始數(shù),比如由123可以產(chǎn)生出132,213,231,312,321這5個(gè)原始數(shù).將這6個(gè)數(shù)相加,得到的和1332稱(chēng)為由原始數(shù)123生成的終止數(shù).利用材料解決下列問(wèn)題:
(1)分別求出由下列兩個(gè)原始數(shù)生成的終止數(shù):243,537;
(2)若一個(gè)原始數(shù)![]() 的終止數(shù)是另一個(gè)原始數(shù)
的終止數(shù)是另一個(gè)原始數(shù)![]() 的終止數(shù)的3倍,分別求出所有滿(mǎn)足條件的這兩個(gè)原始數(shù).
的終止數(shù)的3倍,分別求出所有滿(mǎn)足條件的這兩個(gè)原始數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某學(xué)校小組利用暑假中前40天參加社會(huì)實(shí)踐活動(dòng),參與了一家網(wǎng)上書(shū)店經(jīng)營(yíng),了解到一種成本每本20元的書(shū)在x天銷(xiāo)售量P=50﹣x.在第x天的售價(jià)每本y元,y與x的關(guān)系如圖所示. 已知當(dāng)社會(huì)實(shí)踐活動(dòng)時(shí)間超過(guò)一半后.y=20+ ![]()

(1)請(qǐng)求出當(dāng)1≤x≤20時(shí),y與x的函數(shù)關(guān)系式,并求出第12天此書(shū)的銷(xiāo)售單價(jià);
(2)這40天中該網(wǎng)點(diǎn)銷(xiāo)售此書(shū)第幾天獲得的利潤(rùn)最大?最大的利潤(rùn)是多少?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com